Mouvement circulaire uniforme : accélération
Durée : 6 mn
Note maximale : 6
Question
Par rapport à un référentiel terrestre, la lune (assimilée à un point matériel) décrit une trajectoire circulaire d'un mouvement uniforme.
Utilisez la géométrie pour déterminer la direction et le sens de l'accélération de la lune.
Solution
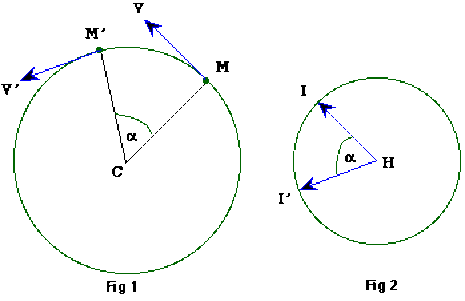
Soient \(M\) et \(M'\) les positions de la Lune à deux instants successifs t et t' et les vecteurs vitesses
\(\vec{V}=\vec{v}(M)\) et \(\vec{V'}=\vec{v}(M')\)(voir Fig 1).
On a vu que, lorsque leur origine commune est en \(H\), leurs extrémités \(I\) et \(I'\) se trouvent sur l'hodographe : un cercle de centre \(H\) dans le cas d'un mouvement circulaire uniforme (voir Fig 2).
(2 points)
L'accélération moyenne entre ces deux instants est égale à
\(\frac{\vec{II'}}{(t'-t)}\)
(1 point)
Les triangles \(MCM'\) et \(IHI'\) sont isocèles et leurs côtés égaux sont perpendiculaires deux à deux : il en est de même de leurs bases \(MM'\) et \(II'\).
(1 points)
L'accélération moyenne est donc perpendiculaire à la vitesse moyenne
\(\frac{\vec{MM'}}{(t'-t)}\)
(1 point)
Ceci reste vrai lorsque l'intervalle de temps \(t'- t\) devient infiniment petit.L'accélération instantanée est donc perpendiculaire à la vitesse instantanée : elle est portée par le rayon \(CM\).
On voit à l'aide des schéma qu'elle est orientée dans le même sens que le vecteur \(\vec{MC}\): elle est donc centripète.
(1 point)