Coordonnées polaires : vitesse
Durée : 9 mn
Note maximale : 9
Question
Calculez le vecteur vitesse en chaque point \(M\) de la trajectoire définie dans le plan \(xOy\) par la relation \(r = 2R \cos\varphi \quad (R > 0)\) en coordonnées polaires :
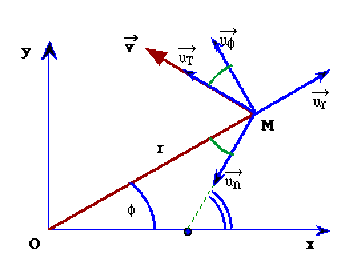
\(r=|\vec{OM}|\),\(\varphi=(\vec{u_x},\vec{OM})\)
Trouvez le vecteur unitaire \(\vec{u_T}\) porté par la tangente à la trajectoire au point \(M\) et orienté dans le sens du mouvement ainsi que \(\vec{u_N}\) vecteur unitaire porté par la normale et tel que \(\vec{u_T}\times\vec{u_N}=\vec{u_Z}\).
Solution
On a :
\(\vec{OM}=2R\cos\varphi\vec{u_r}\) et \(\displaystyle{\vec{v}=\frac{d\vec{OM}}{dt}}\)
(1 point)
Donc :
\(\displaystyle{\vec{v}=2R(-\sin\varphi\frac{d\varphi}{dt}\vec{u_r}+\cos\varphi\frac{d\vec{u_r}}{dt})}\)
avec \(\displaystyle{\frac{d\vec{u_r}}{dt}=\frac{d\varphi}{dt}\vec{u_\varphi}}\)
(2 points)
On obtient finalement,
\(\displaystyle{\vec{v}=2R\frac{d\varphi}{dt}\vec{u_T}}\) avec \(\vec{u_T}=-\sin\varphi\vec{u_r}+\cos\varphi\vec{u_\varphi}\)
où ce dernier est un vecteur unitaire porté par la tangente à la trajectoire au point \(M\) et orienté dans le sens du mouvement si \(\displaystyle{\frac{d\varphi}{dt}>0}\)
(2 points)
Soit le vecteur unitaire \(\vec{u_N}=a\vec{u_r}+b\vec{u_\varphi}\); ses composantes \(a\) et \(b\) sont telles que :
\(\vec{u_N}-\vec{u_T}=0\) et \(\vec{u_T}\times\vec{u_N}=\vec{u_Z}\)
(1 point)
Les composantes \(a\) et \(b\) sont donc les solutions du système d'équations :
\(-a\sin\varphi+b\cos\varphi=0\) et \(-a\sin\varphi-b\cos\varphi=1\)
(2 points)
On trouve : \(\vec{u_N}=-\cos\varphi\vec{u_r}-\sin\varphi\vec{u_\varphi}\).
(1 point)