Coordonnées polaires : accélération
Durée : 9 mn
Note maximale : 9
Question
Rappelez l'expression du vecteur vitesse en chaque point \(M\) de la trajectoire définie dans le plan \(xOy\) par la relation \(r = 2R \cos \varphi \quad(R > 0)\) en coordonnées polaires :
\(r=|\vec{OM}|\),\(\varphi=(\vec{u_x},\vec{OM})\)
Dans le cas particulier où \(\displaystyle{\frac{d\varphi}{dt}}\) est constant, montrez que le mouvement est uniforme.
Calculez le vecteur accélération et exprimez-le en fonction de la vitesse ; identifiez la trajectoire.
Interprétez géométriquement les résultats.
Solution
On a établi précédemment que :
\(\displaystyle{\vec{v}=2R\frac{d\varphi}{dt}\vec{u_T}}\)
avec
\(\vec{u_T}=-\sin\varphi\vec{u_r}+\cos\varphi\vec{u_\varphi}\)
où ce dernier est un vecteur unitaire porté par la tangente à la trajectoire au point \(M\) et orienté dans le sens du mouvement si \(\displaystyle{\frac{d\varphi}{dt}>0}\). On a donc
\(\displaystyle{\vec{v}.\vec{v}=v^2=4R^2\left(\frac{d\varphi}{dt}\right)^2}\)
Si \(\displaystyle{\frac{d\varphi}{dt}}\) est constant, la norme de la vitesse est également constante et le mouvement est uniforme.
(2 points)
On a :
\(\displaystyle{\vec{a}=\frac{d\vec{v}}{dt}=\frac{d}{dt}(v\vec{u_T})=v\frac{d\vec{u_T}}{dt}}\)
(1 point)
où
\(\begin{array}{rcl}\displaystyle{\frac{d\vec{u_T}}{dt}}&=&\displaystyle{\frac{d\varphi}{dt}(-\cos\varphi\vec{u_r}-\sin\varphi\vec{u_\varphi})-\sin\varphi\frac{d\varphi}{dt}\vec{u_\varphi}+\cos\varphi\left(-\frac{d\varphi}{dt}\vec{u_r}\right)}\\&=&\displaystyle{2\frac{d\varphi}{dt}\vec{u_N}=\frac{v}{R}\vec{u_N}}\end{array}\)
et finalement
\(\vec{a}=\frac{v^2}{R}\vec{u_N}\).
(3 points)
La trajectoire est un cercle car l'expression de l'accélération est caractéristique d'un mouvement circulaire uniforme.
(1 point)
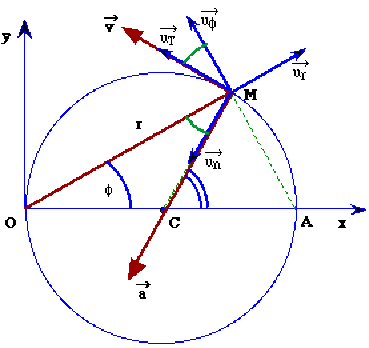
Ceci est confirmé par l'étude géométrique :
si \(M\) est sur un cercle de diamètre \(OA = 2R\), on a \(OM = OA \cos \varphi\) , l'angle \(\displaystyle{(\vec{OM},\vec{AM})=\frac{\pi}{2}}\) et l'angle \(\displaystyle{(\vec{CA},\vec{CM})=2\varphi}\)
ce qui explique que\(\frac{d\vec{u_T}}{dt}=2\frac{d\varphi}{dt}\vec{u_N}\)
(2 points)