Accident de chantier
Durée : 5 mn
Note maximale : 5
Question
Pour démolir un vieux bâtiment, on utilise une masse \(M\) suspendue par un filin au bras d'une grue et on lui imprime un mouvement oscillant qu'on peut assimiler à celui d'un pendule.
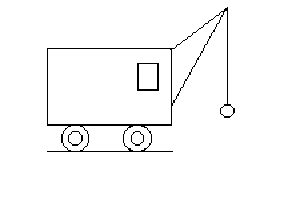
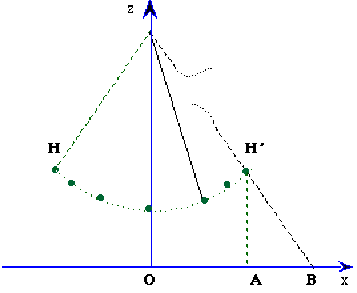
On suppose que le filin se rompt lorsque la masse se trouve dans la position la plus éloignée possible de la verticale, \(H\) ou \(H'\).
Où va-t-elle tomber ? Au point \(A\), ..\(B\) ? Ailleurs ?
Solution
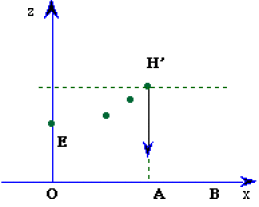
Lorsque la masse \(M\) atteint le point \(H'\), sa vitesse par rapport au référentiel galiléen \(Oxyz\) lié au sol est nulle, car l'abscisse curviligne \(s=EH'\) a une valeur stationnaire en ce point \(\left(\displaystyle{v=\frac{ds}{dt}=0}\right)\).
(1 point)
La masse reste soumise à la seule action de la pesanteur qui s'exerce suivant la direction de la verticale ( celle de l'axe \(Oz\)).
(1 point)
La rupture du filin au même instant, fait disparaître la liaison entre la masse \(M\) et le bras de la grue.
(1 point)
Dans une direction perpendiculaire à \(Oz\), par exemple celle de l'axe \(Ox\) qui appartient au plan d'oscillation, la masse \(M\) est donc libre à partir de cet instant et suivant le Principe d'inertie, elle conserve son état de mouvement. Elle reste donc immobile par rapport à \(Ox\) : elle tombe en \(A\).
(2 points)