La Terre comme référentiel galiléen
Durée : 8 mn
Note maximale : 8
Question
Par rapport à un référentiel lié à son centre \(T\), qu'on peut considérer comme galiléen pendant une durée courte en comparaison d'une année, Képler a établi les lois relatives au mouvement d'un point matériel abandonné à l'action de la Terre :
1) la trajectoire est une ellipse dont un des foyers est situé au point \(T\).
2) la trajectoire est parcourue en respectant la loi des aires :
\(TMv_\bot=TM^2\omega=\mathrm{Cte}\)
où \(\omega\) est la vitesse angulaire de rotation de la demi-droite \([TM)\).
Par ailleurs, l'observation quotidienne de la "chute libre" montre que la trajectoire d'un point matériel abandonné sans vitesse initiale par rapport à la Terre est un segment de droite verticale.
En considérant uniquement le cas où l'expérience est réalisée à l'équateur, examinez dans quelle mesure son résultat est compatible avec les lois de Képler.
Dans quelle mesure peut-on dire de la Terre qu'elle est un référentiel galiléen ?
Solution
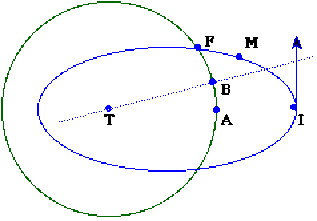
Dans un référentiel galiléen lié à son centre \(T\), la Terre tourne avec une vitesse angulaire \(\Omega\) constante. Le point matériel est abandonné en \(I\), à la verticale de \(A\), sans vitesse par rapport à la Terre donc avec une vitesse angulaire \(\Omega\) par rapport aux étoiles.
(1 point)
Le point matériel décrit donc une ellipse dans le référentiel galiléen
(1 point)
et suivant la loi des aires,
\(TM^2\omega(M)=\mathrm{Cte}\),
\(\omega\) croit depuis \(I\) jusqu'à \(F\) où le point matériel touche le sol :
\(\omega(M)\ge\omega(I) =\Omega\).
(2 point)
Pendant le même temps la verticale \(TA\) a tourné avec la vitesse \(\Omega\) jusqu'à la position \(TB\).
(1 point)
De \(\omega\ge\Omega\), on déduit que
\(AF>AB\)
le point matériel a été dévié vers l'est par rapport à la verticale.
(2 points)
Que la terre puisse être considérée comme un référentiel galiléen dépend de l'amplitude de \(BF\). Elle est général négligeable lorsque \(AI\) est petit devant \(TA\) ou lorsque l'angle \((TA,TB)\ll2\pi\).
(1 point)