Référentiel galiléen lié au centre de la terre
Durée : 5 mn
Note maximale : 5
Question
Dans le référentiel galiléen lié aux étoiles fixes, l'expérience montre qu'un point matériel \(T\) soumis à l'action d'un objet sphérique de centre \(S\), peut rester confiné dans une région finie de l'espace lorsque sa vitesse n'est pas trop grande (c'est la cas de la Terre autour du Soleil). Képler a établi que la trajectoire de \(T\) était une ellipse dont un des foyers était situé au point \(S\).
Ce résultat est-il compatible avec l'hypothèse commune selon laquelle le référentiel lié à \(T\) et animé d'un mouvement de translation par rapport au référentiel galiléen lié aux étoiles, serait galiléen ?
Pouvez-vous expliquer dans quelle mesure le caractère galiléen ou non galiléen de ce référentiel est une propriété limitée dans l'espace ou dans le temps ?
Solution
Le référentiel lié aux étoiles fixes étant galiléen, seuls les référentiels animés par rapport à lui d'un mouvement de translation rectiligne et uniforme, sont également galiléens conformément au Principe d'invariance.
(1 point)
Ce n'est pas le cas du référentiel lié à \(T\) car la trajectoire de \(T\) par rapport au référentiel galiléen lié aux étoiles est une ellipse.
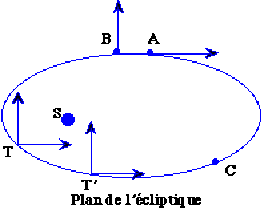
(1 point)
Cependant pour des phénomènes dont la durée est beaucoup plus petite qu'un an (période de révolution), le mouvement de la terre est pratiquement rectiligne et uniforme.
(1 point)
C'est le cas entre \(A\) et \(B\), mais pas entre \(B\) et \(C\).
(1 point)
On peut ainsi attribuer au référentiel terrestre un caractère galiléen avec une bonne approximation dans un intervalle de temps limité et dans une région limitée de l'espace.
(1 point)