Exercice de tir
Durée : 10 mn
Note maximale : 10
Question
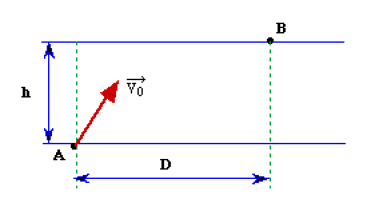
Une cible est abandonnée à l'action de la pesanteur au point \(B\), à une altitude \(h\), sans vitesse initiale. Un tireur posté au sol au point \(A\), à l'altitude \(0\) et à une distance non nulle de la verticale de la cible, est mis au défi de l'atteindre avec un projectile.
En considérant la cible et le projectile comme des points matériels et en raisonnant par rapport au référentiel galiléen où le tireur est immobile (la Terre), examinez comment le tireur doit s'y prendre pour relever le défi de la façon la plus simple et la plus efficace.
Plus précisément, et si on admet que les forces de frottement avec l'air sont négligeables, déterminez dans quelle direction il doit viser s'il décide d'appuyer sur la détente à l'instant même, \(t = 0\), où la cible est abandonnée.
Expliquez pourquoi la vitesse initiale \(|\vec{v_0}|\) du projectile n'est pas un facteur déterminant de la réussite.
Calculez la valeur minimale qu'il faut donner à la vitesse initiale du projectile pour qu'il atteigne la cible avant qu'elle touche le sol.
Solution
Tout point matériel soumis à l'action de la pesanteur subit une accélération uniforme égale à l'accélération de la pesanteur \(\vec{g}\)(identité des masses pesante et inerte).
(1 point)
La trajectoire de chaque point matériel est située dans le plan passant par le point initial et contenant le vecteur \(\vec{g}\) et le vecteur vitesse initial (cas particulier d'un champ uniforme) : on a
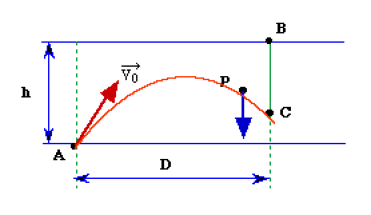
- \(\vec{AP}(t)=\vec{g}\frac{t^2}{2}+\vec{V_0}t\) où \(P\) désigne le point où le projectile se trouve à l'instant \(t\) : la trajectoire du projectile est dans un plan vertical contenant \(\vec{V_0}\)
(1 point)
- \(\vec{BC}(t)=\vec{g}\frac{t^2}{2}\) où \(C\) désigne le point où la cible se trouve à l'instant \(t\) : la trajectoire de la cible est une droite verticale (parallèle à ce plan).
(1 point)
Une condition nécessaire et suffisante pour que le projectile atteigne la cible est que les points \(P\) et \(C\) coïncident à un instant \(T\) : dans ces conditions,
\(\vec{AB}=\vec{AP}(T)-\vec{BC}(T)=\vec{V_0}T\)
La vitesse \(\vec{V_0}\) doit être portée par la droite \(AB\).
Ainsi, s'il appuie sur la détente à l'instant \(t=0\), il suffit au tireur de viser la cible pour être certain que le projectile l'atteindra quelque part sur la verticale passant par le point \(B\).
(2 points)
(1 point)
L'instant \(T\) de l'impact est lié à \(V_0=|\vec{V_0}|\) et à \(D=|\vec{AB}|\) par l'unique relation:
\(D = V_0T\).
(1 point)
Ainsi, la connaissance de la valeur initiale de la vitesse n'est pas une condition de la réussite dans la mesure où il a été seulement imposé au tireur d'atteindre la cible sans préciser à quel instant et donc à quel endroit.
(1point)
Il est entendu cependant que l'impact doit se produire avant que la cible touche le sol. Ceci impose qu'à l'instant \(T\) on ait :
\(|\vec{BC}(T)|=g\frac{T^2}{2}<h\quad(g>0)\)
(1 point)
On en déduit que
\(V_0>D\sqrt{\frac{g}{2h}}\)