Ion dans un champ électrique
Durée : 8 mn
Note maximale : 8
Question
Un point matériel portant une charge \(q (> 0)\) est soumis à l'action d'un champ électrique uniforme \(\vec{E}\): la force qui agit sur lui est égale à \(q\vec{E}\).
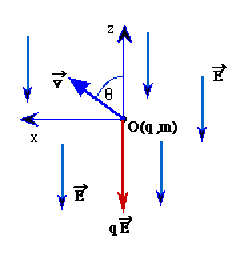
Par rapport au repère \(Oxyz\) , lié à un référentiel galiléen, où \(\vec{E}=E\vec{u_z}\) avec \(E<0\).
établissez les équations du mouvement de ce point matériel de masse \(m\).
Sachant qu'à l'instant \(t = 0\), le point matériel se trouve au point \(O\) et que sa vitesse est
\(\vec{v}(0)=v\sin\theta\vec{u_x}+v\cos\theta\vec{u_z}\) où \(v>0\).
montrez que la trajectoire est située dans un plan : précisez de quel plan il s'agit.
Déterminez sans calcul la nature de la trajectoire.
Solution
L'Equation Fondamentale de la Dynamique s'écrit :
\(q\vec{E}=\frac{m\vec{dv}}{dt}\).
(1 point)
En projetant sur l'axe \(Oz\) du repère, on obtient :
\(\frac{dvz}{dt}=\left(\frac{q}{m}\right)E\)
(1 point)
En projetant sur les axes \(Ox\) ou \(Oy\) on obtient :
\(\frac{dv_{(x \mathrm{ ou } y)}}{dt}=0\)
(1 point)
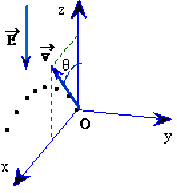
Le mouvement est donc uniforme suivant \(Ox\) et \(Oy\) ; mais comme \(v_y(0) = 0\), le point matériel reste dans le plan \(xOz\).
(2 points)
(1 point)
La trajectoire dans le plan \(xOz\) résulte de la combinaison :
- d'un mouvement uniforme suivant \(Ox\), de vitesse \(v\) \(\sin\theta\),
(1 point)
- d'un mouvement uniformément accéléré, d'accélération \(\left(\frac{q}{m}\right)E<0\) suivant \(Oz\).
La trajectoire est donc un arc de parabole d'origine \(O\).
(1 point)