Cas des planètes
Durée : 8 mn
Note maximale : 8
Question
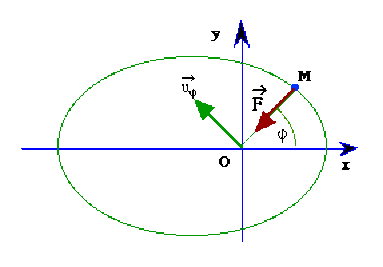
Le mouvement d'un point matériel dans un plan \(xOy\) est décrit en coordonnées polaires:
\(r=OM\), \(\varphi=(\vec{Ox},\vec{OM})\)
Montrez que le mouvement est dû à l'effet d'une force centrale lorsque les coordonnées sont liées par la condition \(r^2\varphi=C\)
La trajectoire est définie par la relation \(r(e\cos\varphi-1)=p\), où \(e\) et \(p\) sont des paramètres caractéristiques.
Montrez que la force est proportionnelle à \(r^n\) et déterminez \(n\).
Solution
On a \(\displaystyle{\vec{v}=\frac{d\vec{OM}}{dt}=d\frac{(r\vec{u_r})}{dt}=\dot{r}\vec{u_r}+r(\dot{\phi}\vec{u_\phi)}}\)
Compte tenu de la condition : \(r^2\dot{\phi}=C\), \(\displaystyle{\vec{v}=\dot{r}\vec{u_r}+\frac{C}{r}\vec{u_\phi}}\)
(2 points)
On a
\(\displaystyle{\vec{a}=\frac{d\vec{v}}{dt}=\ddot{r}\vec{u_r}+C\left(\frac{-\dot{r}}{r^2}\right)\vec{u_\phi}+\dot{r}(\dot{\phi}\vec{u_\phi})+\frac{C}{r}(-\dot{\phi}\vec{u_r})}\)
Compte tenu de la condition, on a
\(\vec{a}=\left(\ddot{r}-\frac{C\dot{\phi}}{r}\right)\vec{u_r}\)
et la force est dirigée suivant \(\vec{OM}\).
(2 points)
En dérivant la relation \(r(1+e\cos\phi)=p\) par rapport au temps, on obtient
\(\dot{r}\left(\frac{p}{r}\right)+r(-e\dot{\phi}\sin\phi)=0\) soit \(\displaystyle{\dot{r}=\left(\frac{Ce}{p}\right)\sin\phi}\)
(2 points)
Puis de nouveau,
\(\displaystyle{\ddot{r}=\left(\frac{Ce}{p}\right)\dot{\phi}\cos\phi}\)
(1 point)
En substituant dans l'expression de l'accélération, on trouve
\(\displaystyle{a=C\dot{\phi}\left(\frac{e\cos\phi}{p}-\frac{1}{r}\right)=C\dot{\phi}\left(\frac{-1}{p}\right)=\left(\frac{C^2}{r^2}\right)\left(\frac{-1}{p}\right)=\left(\frac{C^2}{p}\right)\left(\frac{-1}{r^2}\right)}\)
La force est coulombienne et répulsive.
(1 point)