Impulsion transmise lors d'un demi-tour
Durée : 10 mn
Note maximale : 11
Question
Par rapport à une direction donnée (choisie comme axe \(x'x\)) l'espace est divisé en deux régions. Dans l'une, \(x > 0\), un point matériel de masse \(m\) est libre; dans l'autre \(x<0\), le point matériel est soumis à une force centrale dirigée vers le point \(O\).
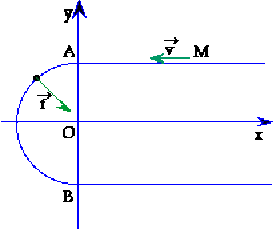
Initialement, le point matériel animé d'une vitesse \(\vec{v}=-v\vec{u_x}\) (\( v > 0\)) se trouve en un point où \(x > 0\). Il atteint le plan \(x = 0\) au point \(A\), situé à la distance \(R\) de \(O\),décrit un demi-cercle de centre \(O\) sous l'effet de la force centrale, et traverse à nouveau le plan \(x = 0\) au point \(B\).
Montrez que la vitesse du point matériel sur le cercle est constante.
Calculer l'impulsion \(\int\vec{f}dt\) entre \(A\) et \(B\), communiquée au point matériel lors de ce demi-tour
Comparer le résultat à la variation de la quantité de mouvement \(\vec{p}=m\vec{v}\) entre \(A\) et \(B\).
Vérifiez qu'on obtient directement cette relation en intégrant l'Equation Fondamentale de la Dynamique.
Solution
Dans le cas d'une trajectoire circulaire,
\(\displaystyle{\vec{a_N}=\frac{v^2}{R}\frac{\vec{MO}}{R}}\) et \(\displaystyle{\vec{a_T}=\frac{d\vec{v}}{dt}}\)
(2 points)
Sous l'effet d'une force centrale, \(\vec{f_T}=\vec{0}\) donc \(\vec{a_T}=\vec{0}\) et \(v^2\) est conservé.
(1 point)
L'impulsion communiquée au point matériel est égale, par définition, à l'intégrale \(\int{\vec{f}dt}\) prise entre \(A\) et \(B\) : soit
\(\int_0^\pi \vec{f}d\alpha/\omega\)
\(\)où \(\alpha=(\vec{Oy},\vec{OM})\) et \(\displaystyle{\omega=\frac{v}{R}}\)
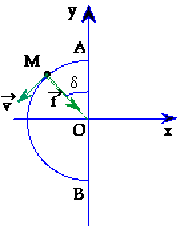
(2 points)
L'impulsion communiquée suivant \(Oy\) est égale à
\(\int{f_ydt}=\int{\vec{f}.\vec{u_y}dt}\)
soit
\(-\frac{mv^2}{\omega R}\int\cos\alpha d\alpha=-mv\int_0^\pi\cos\alpha d\alpha=0\)
(2 points)
Suivant \(Ox\) elle est égale à
\(mv\int_0^\pi{\sin\alpha d\alpha}=2mv\)
(2 points)
L'Equation Fondamentale de la Dynamique s'écrit :
\(\vec{f}=m\frac{d\vec{v}}{dt}\) ou \(\vec{f}dt=md\vec{v}\)
On obtient directement le résultat en intégrant
\(\int_b^a\vec{f}dt=m(\vec{v_b}-\vec{v_a})\)
(2 points)