Collision (1)
Durée : 8 mn
Note maximale : 8
Question
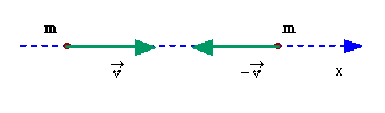
Deux points matériels de même masse \(m\), isolés et n'interagissant pas l'un sur l'autre, sont animés de vitesses opposées \(\vec{v}\) et \(-\vec{v}\) par rapport à un référentiel galiléen.
Ils entrent en collision.
Déterminez les vitesses \(\vec{v_1}\) et \(\vec{v_2}\) des deux points matériels après le choc qu'on supposera élastique.
Représentez les résultats sur un diagramme.
Solution
On considère le système formé par les deux points matériels.
(1 point)
La conservation de la quantité de mouvement totale s'écrit :
\(\vec{P}=\vec{P'}\)
soit \(m\vec{v}+m(-\vec{v})=m\vec{v'}_1+m\vec{v'}_2\).
On a donc \(\vec{v'}_1.\vec{v'}_2=\vec{0}\).
(2 points)
La conservation de l'énergie mécanique totale en l'absence d'interactions internes et externes se réduit à la conservation de l'énergie cinétique :
\(E_c=E'_c\)
soit \(\displaystyle{\left(\frac{mv^2}{2}\right)=\frac{m(v'_1)^2}{2}+\frac{m(v'_2)^2}{2}}\)
On a donc \(v'^2=v^2\)
(2 points)
Sous l'effet de la collision, la trajectoire de chaque point matériel subit une rotation d'angle \(\alpha\) arbitraire et la norme de la vitesse est conservée.
(1 point)
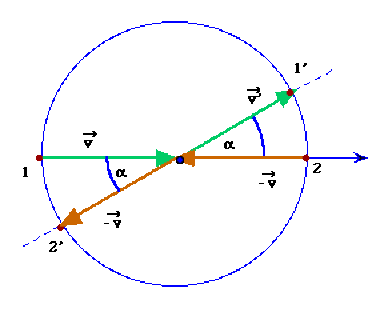
(2 points)