Marcheur sur un plateau mobile
Durée : 8 mn
Note maximale : 7
Question
La vitesse d'un homme par rapport au référentiel lié au solide sur lequel il se déplace en marchant, est invariante et égale à \(v_0\).
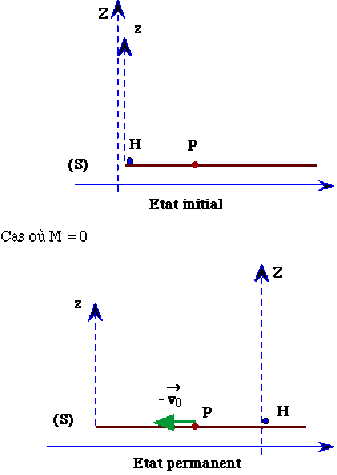
Initialement, cet homme \(H\) est au repos sur un plateau \(P\) immobile par rapport au sol \(S\).
Puis il se met en mouvement : au bout d'un certain temps, sa vitesse \(v_{/P}\) par rapport à \(P\) atteint la valeur \(v_0\).
En supposant que tous les déplacements s'effectuent dans une direction unique et qu'il n'y a pas de frottement entre \(P\) et \(S\), calculez la vitesse \(V_{/S}\) de \(P\) par rapport à \(S\) en fonction de \(m\), masse de \(H\), et de \(M\), masse de \(P\).
On admet que le mouvement de chaque corps est celui d'un point matériel situé au centre de la masse.
Solution
Puisqu'il faut calculer la vitesse de \(P\) par rapport à \(S\), on adopte le point de vue d'un observateur lié à \(S\) considéré comme un référentiel galiléen.
(1 point)
Le système mécanique formé par \(H\) et \(P\) est soumis à des forces dont la résultante est nulle : poids de \(H\) et \(P\) et réaction de \(S\), pas de frottement entre \(P\) et \(S\) (mais l'existence de frottement entre \(H\) et \(P\) est essentielle).
(1 point)
Le Principe Fondamental de la Dynamique appliqué dans \(S\), a pour conséquence la conservation de la quantité de mouvement de \((H,P)\) dans \(S\) :
\(mv_{/S}+MV_{/S}=0\), algébriquement.
(2 points)
Selon la loi galiléenne de transformation des vitesses, on a \(v_{/S}=v_{/P}+V_{/S}\),
on obtient donc \(\displaystyle{V_{/S}=-\frac{mv_0}{(m+M)}}\)
(2 points)
Il y a un "recul" de \(P\), car \(V_{/S}\) est opposée à \(v_0\), ou mise en mouvement de \(P\) par "réaction".
(1 point)