Marcheur sur un plateau mobile (cas limites).
Durée : 8 mn
Note maximale : 8
Question
La vitesse d'un homme par rapport au référentiel lié au solide sur lequel il se déplace en marchant, est invariante et égale à \(v_0\).
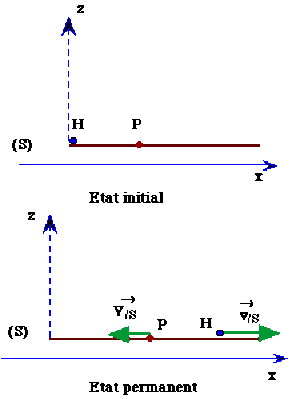
Initialement, cet homme \(H\), de masse \(m\), est au repos sur un plateau \(P\), de masse \(M\), immobile par rapport au sol \(S\). Puis il se met en mouvement : au bout d'un certain temps, sa vitesse \(v_{/P}\) par rapport à \(P\) atteint la valeur \(v_0\).
Déterminez la vitesse \(V_{/S}\) de \(P\) par rapport à \(S\) pour des valeurs remarquables ou limites de la masse \(M\) du plateau (ou du rapport des masses \(\displaystyle{\frac{m}{M}}\)) : comparez les valeurs prévues à celle obtenue par la formule trouvée dans la question précédente.
Solution
La conservation de la quantité de mouvement se traduit par la relation \(mv_{/S}+MV_{/S}=0\)
(1 point)
Comme \(v_{/S}=v_{/P}+V_{/S}\), on obtient
\(\displaystyle{V_{/S}=\frac{m}{(m+M)}v_0}\)
(1 point)
Si la masse \(M\) de \(P\) est très grande devant la masse \(m\) de \(H\) (\(\displaystyle{\frac{m}{M}=0}\), cas d'un porte-avions), on s'attend à un recul négligeable : \(V_{/S}=0\).
On obtient le même résultat par la formule : \(V_{/S}=-v_0\frac{\left(\frac{m}{M}\right)}{\left(\frac{m}{M}\right)+1}\)
(2 points)
Dans la situation inverse (\(\displaystyle{\frac{m}{M}=0}\), cas d'une planche à roulette), on s'attend à \(v_{/S}=0\),
donc \(V_{/S}=-v_{/P}=-v_0\).
(1 point)
On obtient le même résultat par la formule :\(\displaystyle{V_{/S}=\frac{-v_0}{\left(1+\frac{m}{M}\right)}}\)
(1 point)
Dans le cas où les deux masses \(m\) et \(M\) sont égales, on s'attend à une vitesse de "recul" opposée à la vitesse de \(H\), soit
\(V_{/S}=-v_{/S}\) donc \(V_{/S}=-v_{/P}-v_{/S}\)
et finalement \(\displaystyle{V_{/S}=-\frac{v_{/P}}{2}=-\frac{v_0}{2}}\)
Le même résultat est obtenu par application de la formule générale.
(1 point)