Réflexion sur un plan mobile
Durée : 7 mn
Note maximale : 12
Question
On utilise un objet mobile, lourd et plan, pour modifier par réflexion la trajectoire d'un point matériel par rapport à un référentiel galiléen lié au sol (par exemple, une raquette et une balle de ping-pong).
On appelle \(M\) la masse de l'objet, \(\vec{V}\) sa vitesse, perpendiculaire à son plan, \(m\) la masse du point matériel et on suppose que \(M \gg m\).
Le point matériel étant animé par rapport au référentiel galiléen d'une vitesse \(\vec{v}\) le long d'une trajectoire faisant avec la normale au plan de l'objet un angle \(\theta\), déterminez l'angle de réflexion \(\theta'\) après le choc en fonction de \(\vec{v}\) et de la vitesse \(\vec{V}\) de l'objet.
Pour simplifier, on admet que la balle se déplace dans un plan et que l'influence de la pesanteur sur son mouvements est négligeable.
Solution
Par rapport au référentiel galiléen lié au sol, la quantité de mouvement
\(\vec{P}=M\vec{V}+m\vec{v}\) est conservée.
(1 point)
Cette relation, projetée sur la direction normale au plan, devient
\(\vec{P}.\vec{u_x}=MV+mv_x\)
(1 point)
Si on convient d'appeler \(V'\) et \(v'\) les vitesses après le choc, la conservation s'exprime par la relation
\(\displaystyle{V+\frac{mv_x}{M}=V'+\frac{mv'_x}{M}}\)
et si \(M \gg m\) on trouve que \(V' = V\).
(2 points)
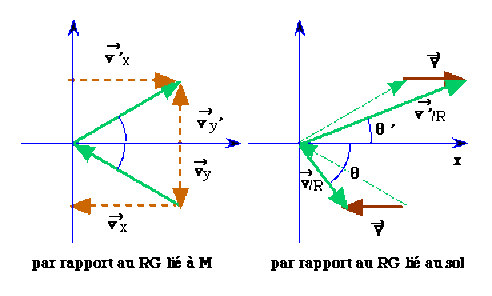
On peut donc lier un référentiel galiléen \(R\) à l'objet et, perpendiculairement au plan, la balle a une vitesse \(v_{x/R} = v_x - V\) donnée par la loi de transformation des vitesses: \(\vec{v}=\vec{v}_{/R}+\vec{V}\)
(1 point)
En projetant sur une direction parallèle au plan, on obtient que \(\vec{P}.\vec{u_y}=MV+mv_y\) est conservé.
Apres le choc on a donc \(v'_y = v_y\) par rapport au sol, puis \(v'_{y/R} = v_{y/R}\) par rapport à \(R\).
(2 points)
Après avoir subi un choc élastique avec \(M\), \(m\) acquiert par rapport à lui une vitesse telle que
\(v'_{x/R} = -v_{x/R}\) et \(v'_{y/R} = v_{y/R}\)
seule solution compatible avec la conservation de l'énergie cinétique.
(2 points)
Sa vitesse par rapport au référentiel galiléen lié au sol est donnée par la loi de transformation :
\(v'_x = v'_{x/R} + V = - v_{x/R} + V = - v_x+ 2V\),
\(v'_y = v'_{y/R} = v_{y/R} = v_y\)
(2 points)
On en déduit que \(|\theta'|<|\theta|\) et plus précisément,
\(\displaystyle{\frac{tg\theta'}{tg\theta}=\frac{v_x}{(-v_x+2V)}}\)
(1 point)