Travail d'une force de tension.
Durée : 8 mn
Note maximale : 8
Question
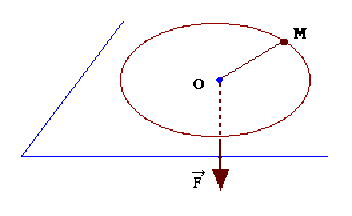
Un point matériel de masse de masse peut se déplacer sans frottement dans un plan horizontal. Il est lié à un point \(O\) de ce plan par un fil inextensible de masse négligeable de longueur \(R\).
On peut faire varier la longueur du fil de façon quasi-statique en le faisant passer à travers le plan par un trou ménagé au point \(O\) et en exerçant sur son extrémité une force d'intensité égale à la tension du fil.
Calculez la variation de vitesse du point matériel lorsqu'on modifie de façon quasi-statique la valeur de \(R\) depuis \(R_1\) à \(R_2\).
Calculez dans les mêmes conditions la variation d'énergie cinétique.
Solution
La force que le fil exerce sur le point matériel pour le maintenir sur le cercle est centrale, \(\vec{F}=F\vec{u_r}\): ainsi, le moment de cette force par rapport à l'axe \(Oz\) est tel que \(\Gamma_z=(\vec{r}\wedge\vec{F}).\vec{u_z}=0\).
(2 points)
Comme \(\displaystyle{\frac{dL_z}{dt}=\Gamma_z}\). \(L_z\) est donc conservé.
(1 point)
Lorsque le point matériel se déplace sur le cercle de rayon \(R\) avec la vitesse \(v\), on a \(L_z = Rmv\).
(1 point)
Ainsi lorsque le rayon varie de \(R_1\) à \(R_2\), la vitesse devient \(\displaystyle{v_2=v_1\frac{R_1}{R_2}}\).
La vitesse augmente lorsque \(R_2 < R_1\).
(1 point)
En fonction du moment cinétique \(L_z\) par rapport à \(Oz\), l'énergie cinétique du point matériel sur le cercle de rayon \(R\) s'écrit :
\(\displaystyle{T=\frac{{L_z}^2}{2mR^2}}\)
(1 point)
La différence d'énergie cinétique qui résulte de cette modification est :
\(\begin{array}{rcl}\Delta T&=&\displaystyle{T_2-T_1=\frac{{L_z}^2}{2m}\left(\frac{1}{{R_2}^2}-\frac{1}{{R_1}^2}\right)}\\&=&\displaystyle{(T_1{R_1}^2)\left(\frac{1}{{R_2}^2}-\frac{1}{{R_1}^2}\right)}\end{array}\)
(1 point)
En fonction de l'énergie cinétique initiale, on trouve :
\(\displaystyle{\Delta T=T_1\left[\left(\frac{R_1}{R_2}\right)^2-1\right]}\)
L'énergie cinétique augmente lorsque \(R_2 < R_1\).
(1 point)