Travail d'une force entre deux instants
Durée : 5 mn
Note maximale : 5
Question
Un point matériel de masse \(m\) est soumis à l'action d'une force \(\vec{F}\).
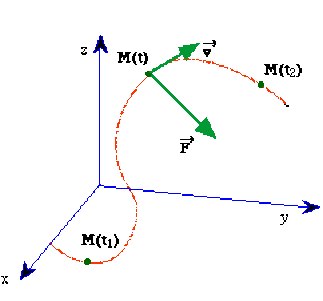
Calculez le travail de \(\vec{F}\) entre deux instants successifs \(t_1\) et \(t_2\) en fonction des vitesses \(\vec{v}\), \(\vec{v_1}\) et \(\vec{v_2}\) du point matériel à ces instants, le long de la trajectoire \(C\) définie par rapport au repère \((O:x,y,z )\) lié à un référentiel galiléen.
Exprimez le résultat sous la forme de l'accroissement d'une grandeur physique que vous définirez.
Solution
Suivant la définition, le travail \(W_C\) de \(\vec{F}\) au cours d'un trajet donné \(C\) est égal à la circulation de \(\displaystyle{W_C=\int_{(C)}\vec{F}_C(M).\vec{dl}}\)
(1 point)
En tout point \(M\) de la trajectoire, la Loi Fondamentale de la Dynamique s'écrit
\(\displaystyle{\vec{F}=m\frac{d\vec{v}}{dt}}\)
par rapport aux axes \((O:x,y,z)\) liés à un référentiel galiléen.
(1 point)
On a donc, le long de la trajectoire et entre les instants \(t_1\) et \(t_2\) :
\(W_C=\int_{t_1}^{t_2}m\frac{d\vec{v}}{dt}.\vec{v}.\vec{dt}=\int_{t_1}^{t_2}m\vec{v}.\vec{dv}=\frac{m}{2}({v_2}^2-{v_1}^2)\)
(2 points)
\(W_C\) apparaît ainsi comme l'accroissement d'une grandeur, dépendant de la norme de la vitesse du point matériel, appelée énergie cinétique :
\(\displaystyle{T=\frac{mv^2}{2}}\)
(1 point)