Bille sur un plan incliné
Durée : 5 mn
Note maximale : 8
Question
Une bille qu’on peut assimiler à un point matériel est abandonnée sans vitesse initiale sur un plan incliné formant avec le plan horizontal un angle dièdre égal à \(\alpha\).
Ecrivez la relation exprimant la conservation de l’énergie mécanique et montrez comment on peut en déduire l’équation horaire du mouvement lorsque le frottement est négligeable.
Montrez qu’on peut aussi retrouver l’Equation fondamentale de la dynamique par cette voie.
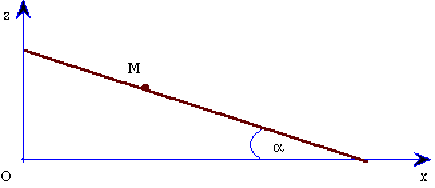
Solution
La bille est soumise à l'action de la pesanteur et à la réaction du plan qui est normale à sa surface en l'absence de frottement.
(2 points)
Ainsi, seul le poids travaille et comme il dérive du potentiel \(U(z) = mgz + U_0\),
on peut écrire \(\displaystyle{W_g=mg(z_0-z)=\frac{mv^2}{2}}\), ce qui exprime la conservation de l'énergie mécanique \(\displaystyle{E=\frac{mv^2}{2}+mgz+U_0}\)
(2 points)
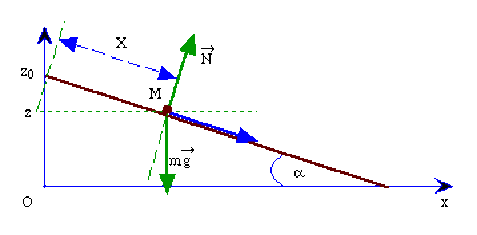
Si on repère par \(X\) la position du point matériel à l'intersection du plan incliné et du plan \(xOz\) contenant , la conservation de l'énergie mécanique permet d'écrire :
\(v^2 = 2g \sin\alpha X\),
la vitesse étant nulle au sommet du plan incliné pris comme origine.
(1 point)
Donc \(v=X=\sqrt{2g\sin\alpha X}\) ou bien \(\displaystyle{\frac{dX}{\sqrt{X}}=\sqrt{2g\sin\alpha}dt}\)
(1 point)
La solution est \(\displaystyle{X=g\sin\alpha\frac{t^2}{2}}\)
si le point matériel se trouve au sommet du plan incliné à l'origine des temps.
(1 point)
En dérivant \(v^2\) par rapport au temps, on retrouve l'Equation fondamentale de la dynamique :
\(2v\dot{v}=2g\sin\alpha v\) soit \(\ddot{X}=g\sin\alpha\).
(1 point)