Réflexion sur 2 miroirs plans faisant un angle entre eux
Partie
Question
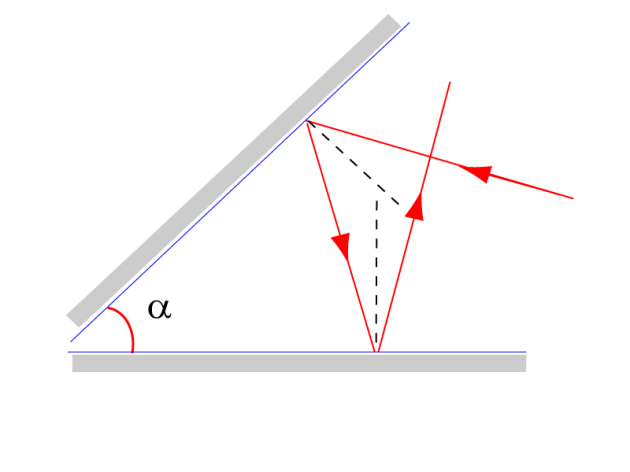
Un rayon lumineux tombe sur un système de deux miroirs plans dont les faces réfléchissantes font un angle \(\alpha=45°\).
Calculer l'angle que fait le rayon deux fois réfléchi avec le rayon incident.
Généraliser pour une valeur quelconque de \(\alpha\).
Utiliser les lois de la réflexion sur un miroir plan.
Aide simple
Évaluer les déviations subies par les rayons.
Aide détaillée
Calculer la déviation que produit le premier miroir sur le rayon incident puis la déviation que produit le deuxième miroir sur le rayon ayant subi une première réflexion sur le premier miroir.
Rappel de cours
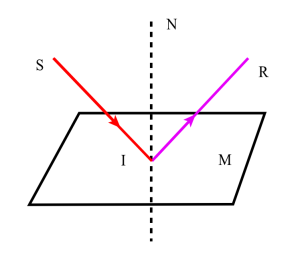
Utiliser les lois de la réflexion de Snell-Descartes :
Le rayon réfléchi est dans le plan d'incidence
L'angle de réflexion est égal à l'angle d'incidence
Ces deux lois sont équivalentes à :
Le rayon réfléchi et le rayon incident, orientés dans le sens de la lumière, sont symétriques par rapport au plan tangent au miroir au point d'incidence.
(valable quelle que soit la la surface réfléchissante)
Solution simple
\(D1=2(\frac\pi2-i1) ;D2=2(\frac\pi2-i2)\)
le rayon incident IA a donc tourné d'un angle : \(D=2(\frac\pi2-i1)+2(\frac\pi2-i2)=2\pi-2(i1+i2)\)
or \(\alpha+(\frac\pi2-i1)+(\frac\pi2-i2)=\pi\) soit : \(\alpha=i1+i2\)
on en déduit : \(D=2\pi-2(i1+i2)=2\pi-2\alpha\)
si \(\alpha=\frac\pi4\) alors \(D=2\pi-2\frac\pi4=2\pi-\frac\pi2=3\frac\pi2\)
Solution détaillée
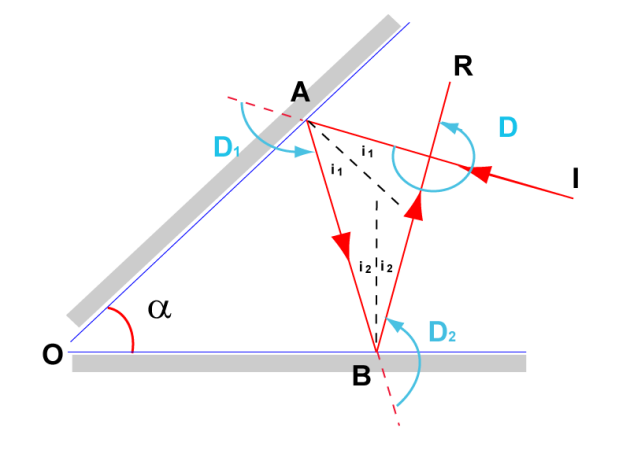
Calculons la déviation que produit le premier miroir sur le rayon incident IA : \(D1=2(\frac\pi2-i1)\) puis la déviation que produit le deuxième miroir sur le rayon AB : \(D2=2(\frac\pi2-i2)\) le rayon incident IA a donc tourné d'un angle : \(D = D1 + D2\) soit \(D=2(\frac\pi2-i1)+2(\frac\pi2-i2)=2\pi-2(i1+i2)\)
Considérons le triangle OAB: la somme des angles de ce triangle vaut \(\pi\), donc \(\alpha+(\frac\pi2-i1)+(\frac\pi2-i2)=\pi\) soit : \(\alpha=i1+i2\) on en déduit : \(D=2\pi-2(i1+i2)=2\pi-2\alpha\) si \(\alpha=\frac\pi4\) alors \(D=2\pi-2\frac\pi4=2\pi-\frac\pi2=3\frac\pi2\)
le rayon incident a tourné de \(3\frac\pi2\) ce qui signifie que rayon incident et rayon réfléchi font entre eux un angle droit: c'est le principe de l'équerre optique.