Prisme rectangle isocèle
Partie
Question
On considère un prisme rectangle isocèle ABC, rectangle en A, d'indice n=1,5.
Tracer la marche du rayon incident à travers le prisme et calculer la déviation du rayon incident à la traversée du prisme dans chacun des cas suivants (on indiquera le ou les cas où il y a réflexion totale).
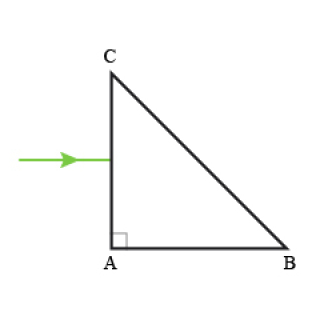
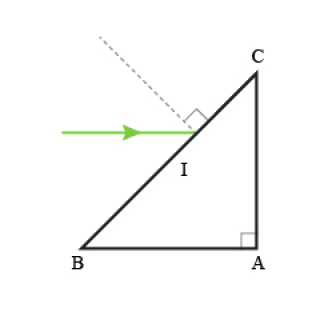
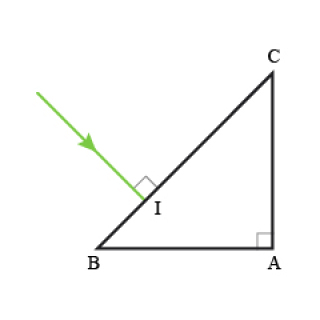
Appliquer les lois de la réfraction.
Aide simple
Calculer la valeur de l'angle limite
Rappel de cours
Le rayon réfracté est dans le plan d'incidence, le rayon incident et le rayon réfracté étant de part et d'autre de la normale au point d'incidence.
Pour chaque lumière monochromatique, il existe un rapport constant positif, entre les sinus des angles d'incidence et de réfraction :
\(\frac{\sin i_1}{\sin i_2}=n_{2,1}=\frac{n_2}{n_1}\)
Un rayon lumineux peut toujours passer d'un milieu transparent dans un autre plus réfringent que le premier. Dans ce cas il se rapproche de la normale (sauf si l'angle d'incidence est nul). L'angle de réfraction est au maximum égal à la valeur de l'angle limite \(\lambda\) défini par :
\(\sin\lambda=\frac{n_1}{n_2}\) avec \(\lambda < 90°\)
Solution simple
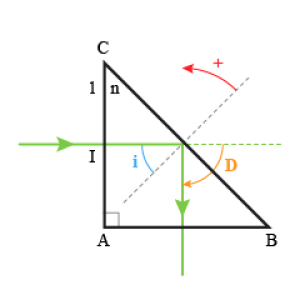
\(D=-\frac\pi2\)
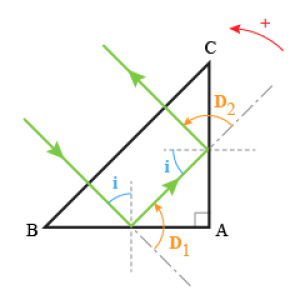
\(D=17°-9°=-26°\)
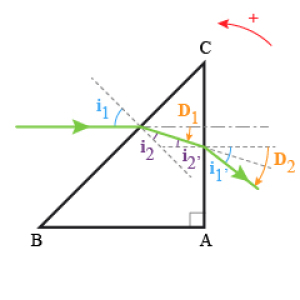
Le faisceau incident revient parallèlement à lui-même.
Solution détaillée

Compte-tenu des caractéristiques du prisme l'angle d'incidence i vaut 45°. Calculons l'angle limite du verre sur l'air :
\(n\sin\lambda=1\)
\(\sin\lambda=\frac1n=\frac1{1,5}\Rightarrow\lambda=41,8°\)
l'angle d'incidence \(i\) est supérieur à l'angle limite \(\lambda\) et il y a donc réflexion totale. La déviation du faisceau vaut : \(D=-\frac\pi2\)

L'angle d'incidence sur la face \(BC\) vaut : \(i_1=45°\) soit si \(\sin i_1=n\cdot\sin i_2\)
\(\sin i_2=\frac{\sin45}{1,5}\) ; \(i_2=28°12'\)
\(D_1=-\left(\frac\pi4-i_2\right)=-17°\) or \(i'_1=D_1\) ; \(n\cdot\sin i'_1=\sin i'_2\), \(i'_2=26°\);
\(D_2=-(i'_2-i'_1)=-9°\) la déviation totale du faisceau vaut donc: \(D=17°-9°=-26°\)

Les angles d'incidence \(i\) valent 45° et sont donc supérieurs à l'angle limite \(\lambda\): il y a donc réflexion totale et \(D=D_1+D_2=\pi\)
Le faisceau incident revient parallèlement à lui-même. C'est une propriété utilisée dans les coins réflecteurs.