Caractéristiques de l'image d'un objet donnée par une lentille (9)
Partie
Question
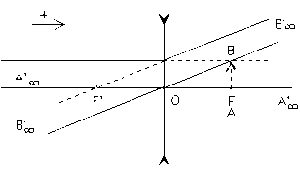
Trouver la position (par rapport au centre optique de la lentille) et la taille (grandissement) de l'image \(A'B'\) d'un objet \(AB\) \((AB = 1 cm)\), par construction géométrique, puis par les formules de conjugaison.
Le sens de propagation de la lumière, de gauche à droite, est choisi comme sens positif. La distance focale de la lentille est \(f\), son centre optique est \(O\). A.N : \(f = -10 \textrm{cm}\) ; \(OA = + 10 \textrm{cm}\)
Positionner les foyers et utiliser des rayons particuliers.
Aide simple
Utiliser les formules de conjugaison avec origine au centre.
Rappel de cours
Tout rayon passant par le centre optique d'une lentille mince n'est pas dévié.
Tout rayon incident parallèle à l'axe principal émerge de la lentille en passant par le foyer principal image.
Tout rayon incident passant par le foyer objet émerge de la lentille parallèlement à l'axe principal.
Pour une lentille sphérique mince, il existe deux plans focaux symétriques par rapport à la lentille: le plan focal objet et le plan focal image. Ces plans comme les foyers qui les forment sont réels pour une lentille convergente et virtuels pour une lentille divergente.
Une lentille mince est optiquement définie par sa distance focale.
Les relations de conjugaison :
origine au centre
\(-\frac1{\overline{OA}}+\frac1{\overline{OA'}}=\frac1{f'}\)
\(\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{OA'}}{\overline{OA}}=\frac{p'}p\)
origine aux foyers
\(\overline{FA}=x\) et \(\overline{F'A'}=x'\)
\(x\cdot x'=-f'^2\)
\(\gamma=\frac{f'}x=-\frac{x'}{f'}\)
Solution détaillée
\(f = -10 \textrm{cm}\)
\(\overline{SF'}=-10\textrm{cm}=\overline{OF'}\)
\(\overline{OA}=+10\textrm{cm}\)
\(\frac1{\overline{OA'}}=-\frac1{10}+\frac1{10}=0\)
l'image est rejetée à l'infini.