Grossissement
Partie
Question
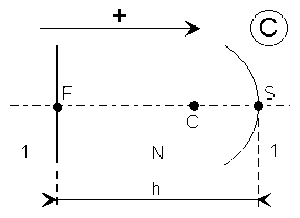
Quelle devrait être la hauteur totale \(h\) d'une loupe épaisse comprenant un dioptre plan et un dioptre sphérique de rayon \(R =\overline{SC}\) séparé par un même milieu (H.T.I.) d'indice N relatif à l'air pour que son plan focal objet, réel, soit confondu avec la surface du dioptre plan. A.N. : \(R = -2 \textrm{cm}, N = 1,5\).
Utiliser l'équation du dioptre sphérique
Aide simple
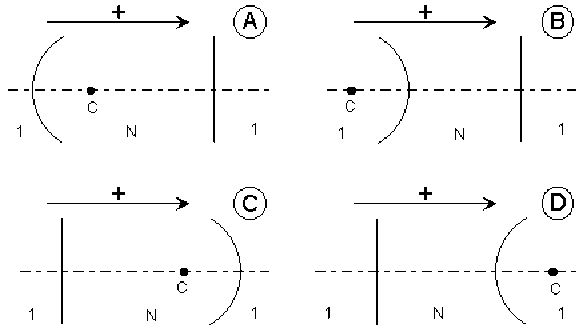
Schématiser les quatre dispositions et natures possibles des deux dioptres constituant cette loupe en choisissant une propagation gauche-droite de la lumière. (2min. sinon passer à l'aide 2). Vérifier que 3 de ces dispositions ne permettent pas un foyer objet réel.
Aide détaillée
Les schémas \(A\) et \(B\) sont à écarter : le plan focal objet confondu avec le dioptre plan se trouverait en position virtuelle ce qui est contraire à l'hypothèse.
Les points de la surface du dioptre plan sont leur propre image par ce dioptre. L'intersection de ce plan avec l'axe doit être foyer objet \(F\) du dioptre sphérique pour que ce plan soit le plan focal objet de la loupe. Cela élimine le schéma \(D\) dont le dioptre sphérique a un foyer objet virtuel.
Rappel de cours
Formules de conjugaison : | |
Origine au sommet | \(\frac{n_1}{\overline{SA_1}}-\frac{n_2}{\overline{SA_2}}=\frac{n_1-n_2}{\overline{SC}}\) \(\gamma=\frac{n_1}{n_2}\frac{\overline{SA_2}}{\overline{SA_1}}\) |
Origine au centre | \(\frac{n_1}{\overline{CA_2}}-\frac{n_2}{\overline{CA_1}}=\frac{n_1-n_2}{\overline{CS}}\) \(\gamma=\frac{\overline{A_2B_2}}{\overline{A_1B_1}}=\frac{\overline{CA_2}}{\overline{CA_1}}\) |
Origine aux foyers | \(\overline{FA_1}~\overline{F'A_2}=\overline{SF}\quad\overline{SF'}=ff'\) \(\gamma=-\frac f{\overline{FA_1}}=\frac{\overline{F'A_2}}{f'}\) |
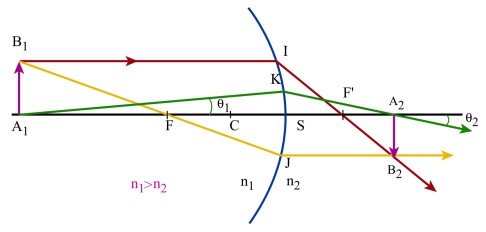
Relation de Lagrange-Helmholtz : \(n_1~\overline{A_1B_1}~\theta_1=n_2~\overline{A_2B_2}~\theta_2\)
Solution détaillée
Le point \(F\) à la surface du dioptre est sa propre image par le dioptre. Si \(F\) est foyer objet de la loupe, il est aussi foyer objet du dioptre sphérique de rayon \(R =\overline{SC}\) séparant le milieu d'indice \(n_1 = N\), de l'air d'indice \(n_2 = 1\).
Pour tout dioptre sphérique : \(f=\frac{n_1}{n_1-n_2}\cdot\overline{SC}\) soit ici \(f=\overline{SF}=\frac N{N-1}\cdot\overline{SC}=-h\).
A.N. : \(h = -\left(\frac{1,5}{0,5}\right)\cdot(-2)=6 \textrm{cm}\quad h=6\textrm{cm}\)