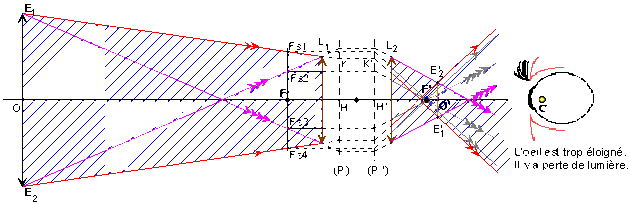
Construction de l'émergent d'un rayon incident quelconque
Partie
Question
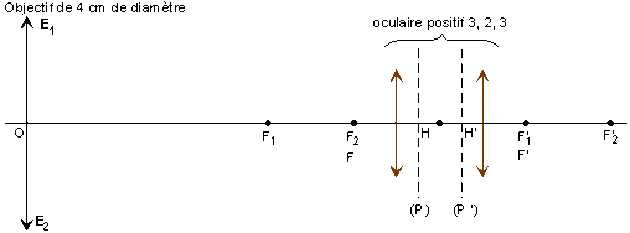
Construire le cercle oculaire \((O')\) de l'instrument schématisé ci-dessous. \(F\) et \(F'\) sont les foyers objet et image de l'oculaire.
Que peut-on dire :
de la distance \(\overline{F'0'}\) du cercle oculaire au plan focal image de l'oculaire
du rapport de cette distance \(\overline{F'O'}\) à la distance focale image \(f'\) de l'oculaire ?
Justifier l'utilité de faire coïncider la pupille de l'œil avec le cercle oculaire.
Pensez à l'image de la monture de l'oculaire.
Aide simple
Le cercle oculaire est le contour de l'image, par l'oculaire, de la surface du dioptre d'entrée de la lumière dans l'instrument. Cette surface objet est circulaire et de diamètre égal à la lentille frontale de l'objectif.
Les rayons issus de l'objectif, qui entrent dans l'oculaire, ont des inclinaisons limites. Les rayons émergents conjugués de ces rayons incidents déterminent les limites du faisceau lumineux émergent ainsi que les extrémités \(E'_1E'_2\) d'un diamètre du cercle oculaire .
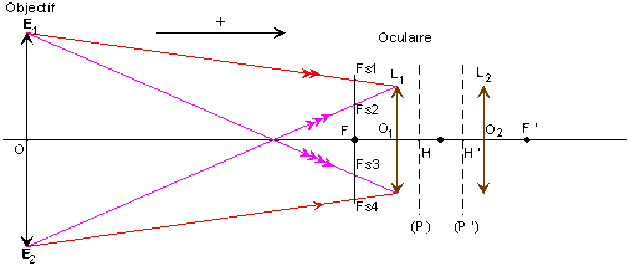
Aide détaillée
Il faut utiliser la technique de construction du rayon émergent d'un rayon incident quelconque. Les images des foyers secondaires \(F_{s1}, F_{s2}, F_{s3}, F_{s4}\) de l'oculaire sont à l'infini. Le support du rayon émergent, conjugué du rayon incident \(E_1F_{s1}\) qui se dirige vers l'image à l'infini de \(F_{s1}\), passe par un point connu du plan principal image \((P')\).
Rappel de cours
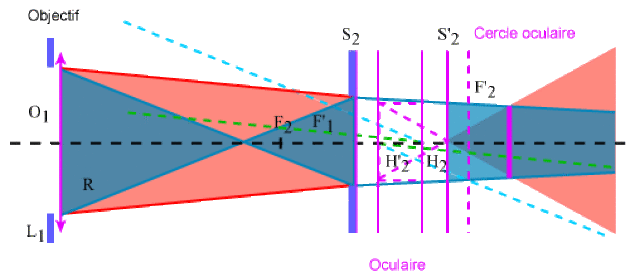
La face d'entrée de l'objectif constitue le diaphragme d'ouverture de l'instrument et la pupille de sortie ou cercle oculaire est l'image[1] de la monture de l'objectif à travers l'oculaire. Il faudra donc placer la pupille de l'oeil dans le plan du cercle oculaire de manière à ce que l'oeil reçoive le flux lumineux maximum ; un oeilleton à la sortie de l'oculaire permet d'y placer l'oeil à cet effet.
Si \(C'\) est le centre du cercle oculaire, en appliquant la formule de Newton on a :
\(\overline{F'_{\mathit2}C'}=-\frac{f_{\mathit2}^2}{\overline{F_{\mathit2}O_{\mathit2}}}=-\frac{f_{\mathit2}^2}{\overline{F_{\mathit2}F'_{\mathit1}}~+~\overline{F'_{\mathit1}O_{\mathit2}}}\approx\frac{f_{\mathit2}^2}{f_{\mathit1}}=\frac{f_{\mathit2}}{f_{\mathit1}}~.~f_{\mathit2}\)
Comme \(f_{\mathit2}/f_{\mathit1}\) est petit devant 1, \(F'_{\mathit2}C'\) sera petit devant \(f_{\mathit2}\). On en déduit donc que le cercle oculaire est au delà mais très près du plan focal image de l'oculaire.
On pourra alors confondre le plan du cercle oculaire avec le plan focal image de l'oculaire et le plan de la pupille de l'oeil. Le diamètre O' du cercle oculaire est donné par :
\(O'=\frac{R'}R=\frac{F'_{\mathit2}C'}{f_{\mathit1}}\approx\frac{f_{\mathit2}}{f_{\mathit1}}\)
soit : \(O'=O~.~\frac{f_{\mathit2}}{f_{\mathit1}}\)
le diamètre du cercle oculaire d'une lunette astronomique est en général inférieur au diamètre de la pupille de l'oeil.
Le grossissement[2] de la lunette est donné par :
\(G=\frac{\alpha'}{\alpha}=f_{\mathit1}~.~P_{\mathit2}=\frac{P_{\mathit2}}{P_{\mathit1}}\)
c'est à dire le produit de la distance focale[3] (en mètres) de l'objectif par la puissance[3] (en dioptries) de l'oculaire.
Dans le cas d'une lunette afocale la puissance de l'oculaire est sa puissance intrinsèque et l'on a rigoureusement :
\(G=\frac{f_{\mathit1}}{f_{\mathit2}}=\frac R{R'}=\frac O{O'}\)
Si la pupille de l'oeil est dans le plan focal image de l'oculaire c'est-à-dire dans le plan du cercle oculaire la puissance de l'oculaire est encore sa puissance intrinsèque et la formule précédente du grossissement[2] est encore valable. Cette relation donne le grossissement intrinsèque de la lunette.
Solution détaillée
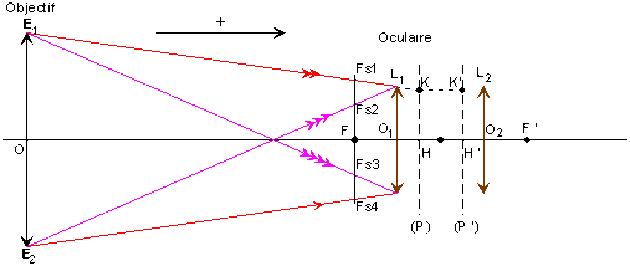
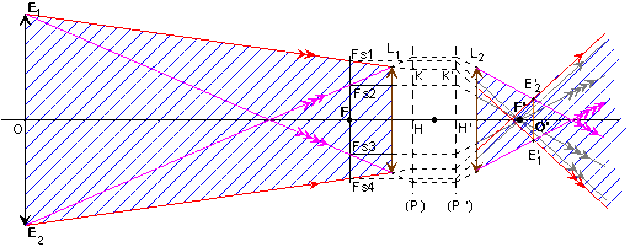
On peut obtenir les rayons émergents des rayons incidents d'inclinaison limite sur l'axe et issus des extrémités \(E_1\) et \(E_2\) d'un diamètre en cherchant les directions des images des foyers secondaires objet \(F_{s1}, F_{s2}, F_{s3}, F_{s4}\).
Le support du rayon émergent, conjugué du rayon incident \(E_1F_{s1}\), contient l'image \(K'\), dans le plan principal image, du point objet \(K\) et se dirige vers l'image à l'infini du foyer secondaire \(F_{s1}\). Les rayons conjugués des autres rayons d'inclinaisons limites (\(E_1F_{s3}\), etc) sont obtenus de la même manière.
Le cercle oculaire c'est-à-dire l'image de la monture de l'objectif est :
en \(O'\), au delà du plan focal image, perpendiculaire à l'axe en \(F'\), mais très près de celui-ci. En effet, la relation de Newton donne :
\(\overline{F'O'}=\frac{-f'^2}{\overline{FO}}=\frac{(<0)}{(<0)}=(>0)\)
à une distance \(\overline{F'O'}\) du plan focal image de l'oculaire d'autant plus faible que le rapport \(FO/ f'\) est élevé en module.
La construction des rayons émergents d'enveloppe de la lumière " entrante " montre que si la pupille s'écarte du cercle oculaire, l'oeil risque de perdre une partie importante de l'" information " lumineuse issue de l'objet observé
Support : Toute trajectoire rectiligne de " rayon lumineux " possède deux parties, une réelle, l'autre virtuelle. En utilisant la notion de droite support de trajectoire l'on inclut nécessairement tous les points possibles de la trajectoire, les points réels et les points virtuels, sans avoir à préciser cette information que l'on ne connait pas nécessairement à l'avance.