Définitions
Bipoint - Segment orienté - Relation d'équivalence
Bipoint
Un bipoint noté \((A,B)\) est un couple ordonné de points. Le bipoint \((A,B)\) est donc différent du bipoint \((B,A)\).

Segment orienté
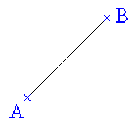
Un segment noté \([A,B]\) est l'ensemble des points de la droite \(AB\).
D'après cette définition : \([A,B] = [B,A]\).
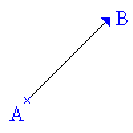
Un segment orienté \([\overrightarrow{A,B}]\) est un segment sur lequel la flèche est orientée de \(A\) (origine) vers \(B\) (extrémité).
Comme pour le bipoint \([\overrightarrow{A,B}]\) est différent de \([\overrightarrow{B,A}]\).
Relation d'équivalence
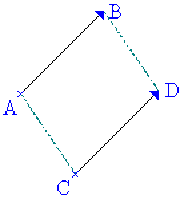
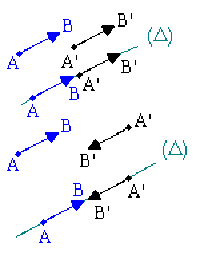
Deux segments orientés \([\overrightarrow{A,B}]\) et \([\overrightarrow{C,D}]\) sont équipollents ou égaux, s'ils ont
même direction,
même sens
et même longueur.
Pour l'ensemble des segments orientés l'équipollence est une relation d'équivalence. Par convention, deux segments orientés équipollents ne sont pas différenciés et appartiennent à une même classe d'équivalence. Ils peuvent donc être représentés par un même vecteur.
Nous adopterons la notation suivante :
Un bipoint \((A,B)\) ou un segment orienté \([\overrightarrow{AB}]\) sera représenté par le vecteur \(\overrightarrow{AB}\) (ou par une lettre surmontée par une flèche \(\overrightarrow{U}\)).
Relation d'équivalence
Définition :
On dit qu'une relation sur \(E\) est une relation d'équivalence si elle est réflexive, symétrique et transitive sur \(E\).
Exemple :
Dans l'ensemble des segments du plan, la relation "avoir même longueur que" est une relation d'équivalence.
Réflexivité
Définition :
On dit que \(R\) est une relation réflexive sur \(E\) si tout élément de \(E\) est en relation avec lui-même c'est à dire : \(\forall x \in E, x ~R x\).
Exemple :
Sur l'ensemble des segments de droite la relation "avoir même longueur que" est une relation réflexive.
Symétrie
Définition :
On dit que \(R\) est une relation symétrique sur \(E\) si pour tout couple \((x,y)\) de \(E \times E\) tel que \(x~ R ~y\) on a aussi \(y ~R ~x\).
Exemple :
Dans l'ensemble des droites du plan la relation "est parallèle à" est une relation symétrique.
Transitivité
Définition :
On dit que \(R\) est une relation transitive sur \(E\) si pour tout triplet \((x,y,z)\) tel que \(x ~R ~y\) et \(y ~R~ z\) on ait aussi \(x ~R ~z\).
Exemple :
Dans \(R\), la relation "est inférieur ou égal à" est une relation transitive.
Norme - Intensité - Module
Une unité de longueur ayant été choisie sur la droite \((\Delta)\) support du vecteur \(\overrightarrow{AB}\), on appelle longueur (ou norme, intensité, module ou valeur absolue) du vecteur \(\overrightarrow{AB}\), désignée par \(\Arrowvert \overrightarrow{AB} \Arrowvert\) la distance \(AB\).
Cas particulier : si \(\Arrowvert \overrightarrow{AB} \Arrowvert = 1\), le vecteur est dit unitaire.
Mesure algébrique
On appelle axe une droite support orientée.
La mesure algébrique d'un vecteur \(\overrightarrow{AB}\), notée \(\overline{AB}\), porté par un axe est le nombre relatif dont la valeur absolue est la longueur du vecteur et définie par :
\(\overline{AB} = AB\) si \(\overrightarrow{AB}\) a pour sens le sens positif de l'axe orienté.
\(\overline{AB} = -AB\) si \(\overrightarrow{AB}\) a pour sens le sens négatif de l'axe orienté.
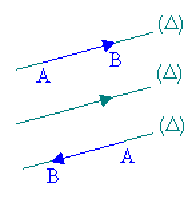
Deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont dits opposés si leurs supports sont parallèles et leurs mesures algébriques comptées sur le même axe \((\Delta)\) sont opposées.
Cas particulier : \(\overrightarrow{AB}\) et \(\overrightarrow{BA}\) sont deux vecteurs opposés.
L'abscisse d'un point \(A\) d'un axe est la mesure algébrique du vecteur \(\overrightarrow{OA}\), \(O\) étant un point de l'axe que l'on choisit pour origine. La connaissance de l'abscisse suppose que l'on a fixé l'origine \(O\), l'axe \((\Delta)\) et l'unité de longueur .

Vecteur libre - Vecteur lié - Vecteur glissant
Vecteur libre
Définition :
Un vecteur est appelé "vecteur libre" s'il est défini par sa direction, son sens et sa longueur.
Exemple :
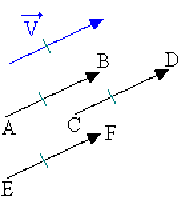
Les vecteurs\( \overrightarrow{AB}\), \(\overrightarrow{CD}\) et \(\overrightarrow{EF}\) sont des représentants d'un même vecteur \(\overrightarrow{V}\).
Vecteur glissant
Définition :
Un vecteur est nommé "vecteur glissant" si l'on impose sa droite support \((\Delta)\).
Exemple :
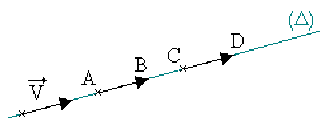
Les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont des représentants du vecteur glissant \(\overrightarrow{V}\).
Vecteur lié
Définition :
Un vecteur est nommé "vecteur lié" si l'on fixe le point d'application \(A\).
Exemple :
La position du vecteur est complètement définie sur la droite support \((\Delta)\).

Deux vecteurs liés d'origines différentes (d'origine \(A\) et \(A'\)) sont :
égaux s'ils ont même direction, même sens et même grandeur.
Ils représentent le même vecteur libre ou le même vecteur glissant s'ils ont même support \((\Delta)\).
opposés s'ils ont même direction, sens opposés, même grandeur et dits "directement opposés" s'ils ont même support \((\Delta)\).