Question 1
Durée : 10 mn
Note maximale : 12
Question
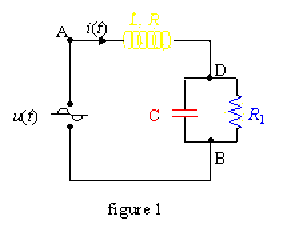
Une bobine d'inductance propre \(L\), de résistance \(R\), en série avec la capacité \(C\), elle-même en parallèle sur la résistance \(R_1\) est parcourue par le courant \(i(t) = I \sqrt{2} \cos \omega t\) \(\left(\omega = 100~ \pi ~\textrm{rad.s}^{-1}\right)\).
Données : \(I = 1 \textrm{ A}\) ; \(L = \textrm{0,2 H}\) ; \(R = 10 \Omega\) ; \(C = 80 \mu \textrm{ F}\); \(R_1 = 25 \Omega\)
Calculer l'impédance \(\underline{Z}\) équivalente du système. Module et argument de \(\underline{Z}\) .
Solution
Calculons l'impédance équivalente du système :
\(\underline{Z} =R + j L \omega + \frac{\frac{-j R_{1}}{C \omega}}{R_{1} - \frac{j}{C \omega}} = R + j L \omega + \frac{R_{1}}{1+jR_{1}C \omega}\)
\(= \frac{R+R_{1} - LCR_{1} \omega^{2} + j \left(L \omega + RR_{1}C \omega\right)}{1 + j R_{1}C \omega}\)
( 4 points )
\(Z = \frac{-\mathrm{4,478} + j \mathrm{69,115}}{1 + j \mathrm{0,628}} = \frac{\underline{N}}{\underline{D}}\)
Module :
\(\arrowvert \underline{Z}\arrowvert = Z = \sqrt{\frac{(\mathrm{4,478})^{2} + (\mathrm{69,115})^{2}}{(1)^{2} + (\mathrm{0,628})^{2}}} = \mathrm{58,65} \Omega\) ( 4 points )
Argument :
\(\textrm{Argument} \left(\underline{Z}\right) = \arg\left(\underline{N}\right) - \arg \left(\underline{D}\right) = \textrm{Arctan}-\frac{\mathrm{69,115}}{\mathrm{4,478}} - \textrm{Arctan} \left(\mathrm{0,628}\right) = \mathrm{61,60}^{\circ}\)
( 4 points )