Définition du logarithme népérien de x [Fonctions logarithmes, exponentielles et puissances]

Définition du logarithme népérien de x

On appelle fonction logarithme népérien^[1], noté ln (ou \(\textrm{log}_{e}\) ), la primitive définie sur \(\mathbb{R}_{+}^{\ast}\) ,de la fonction \(x \mapsto \frac{1}{x}\) s'annulant pour \(x = 1\).

\(\forall x \in \mathbb{R}_{+}^{\ast} \qquad \ln x =\displaystyle{\int_{1}^{x} \frac{dt}{t}}\)

Aire et primitive^[2]

Pour \(x > 1\) : \(\textrm{ln } x > 0\) est l'aire \(A\) limitée par la courbe représentative \(y = 1/t\), l'axe \(Ot\) et les droites d'équations \(t = 1\) et \(t = x\).

Pour \(x = 1\) : \(\textrm{ln }1 = 0\) par définition de la fonction \(\textrm{ln}\).

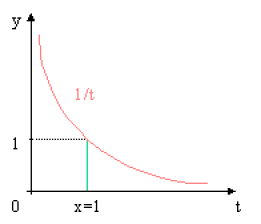
Pour \(0 < x < 1\) : \(\textrm{ln }x < 0\) est l'opposé de l'aire \(A'\) car d'après les propriétés de l'intégrale : \(\displaystyle{\int_{1}^{x} \frac{dt}{t} = - \int_{x}^{1} \frac{d t}{t} = -A '}\)

Notes

népérien
Vient de Jean Néper, mathématicien écossais (1550 - 1617) qui a inventé les logarithmes.
Aire et primitive
Aire
Soit \(f\) une fonction continue et positive sur un intervalle \(I\), \((C)\) sa courbe représentative dans un repère orthogonal \(\left(O ; \vec{i}, \vec{j} \right)\)
L'aire du domaine \(D\) délimité par la courbe \((C)\), l'axe des abscisses et les droites d'équations \(x = a\) et \(x = b\) \((a \le b)\)
L'unité d'aire u est l'aire du rectangle construit avec les vecteurs de base \(\vec{i}\) et \(\vec{j}\)
Aire et primitive
Soit \(f\) une fonction continue et positive sur un intervalle \(I\) et \(a \in I\) ; \(F\) la primitive de \(f\) nulle au point \(a\) \(( F(a) = 0)\).
Pour \(x > a\) et \(x \in I\)
\(\displaystyle{\int_{a}^{x}f(t)dt = F(x) - F(a) = F(x)}\)
donc \(F(x)\) est l'aire du domaine hachuré
Pour \(x > a\) et \(x \in I\)
\(\displaystyle{\int_{a}^{x}f(t)dt = -\int_{a}^{x}f(t)dt =- F(x)}\)
donc \(F(x)\) est l'opposé de l'aire du domaine hachuré