Espace des phases / système Masse-Ressort-Amortisseur.
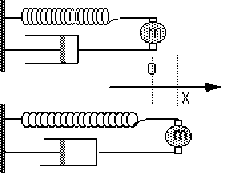
Soit \(X\) la variable (algébrique) qui définit la position de la masse \(m\) : l'origine \(O\) est prise à la position de repos du ressort, i.e. lorsque le système est en équilibre.
Pour modéliser ce problème, on peut admettre que :
La force qu'exerce le ressort est proportionnelle à son allongement, ce qui exige en général que cet allongement soit de faible amplitude par rapport à la longueur du ressort au repos.
La force de rappel exercée sur la masse par le ressort de dureté \(K\) s'exprime alors : \(F = -KX\).
La force exercée par l'amortisseur est linéaire par rapport à la vitesse, soit : \(f = -h.X'\)
Le principe fondamental de la dynamique donne alors : \(m.X'' = - K.X - h.X'\)
Dans le cas où le discriminant du polynôme caractéristique est négatif, et en posant :
\(\lambda = \frac{h}{2m}\) , \(\omega_0^2 = \frac{K}{m} ~\) et \(~ \omega^2 = \frac{K}{m} - \frac{h^2}{4 m^2} = \omega_0^2 - \lambda^2\)
la solution de cette équation différentielle peut se mettre sous la forme :
\(X = A . e^{-\lambda.t} . cos(\omega.t+\varphi)\)
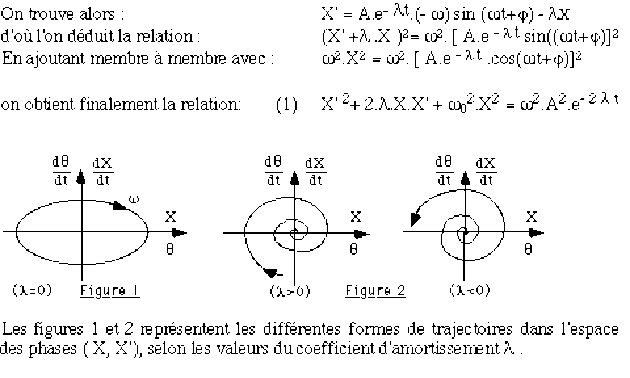
Simulations :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Interprétation :
L'énergie cinétique du système est : \(E_c = \frac{1}{2} m X'^2\)
Son énergie potentielle est égale au travail pour vaincre la force \(F\) exercée par le ressort, soit : \(\displaystyle{E_p = \int_0^x F(x).dx}\)
La relation obtenue ci-dessus peut alors s'exprimer :
\(\frac{1}{2} m X'^2 + \lambda . m . X . X' + \frac{1}{2} K.X^2 = \frac{1}{2} m \omega^2 . A^2 . e^{-2 \lambda t}\)
Le cas où le coeff. d'amortissement \(\lambda\) est nul donne : \(E_p + E_c = \mathrm{constante}\).
La trajectoire elliptique (\(\lambda = 0\)) dans l'espace des phases \((X, X')\) est donc une trajectoire à énergie totale constante.
La convergence vers son centre de la trajectoire spirale (\(\lambda > 0\)) traduit une perte de l'énergie totale du système.
La trajectoire spirale divergente (\(\lambda > 0\)) traduit la croissance de l'énergie totale du système.