Ondes électromagnétiques

Le § A.6.d montre que la condition de réflexion d'une onde électromagnétique sur un dioptre permet de déterminer la forme de l'onde réfléchie. Cependant, bien que les ondes incidentes aient été supposées électromagnétiques et de forme harmonique, le principe de la détermination de l'onde réfléchie reste le même quelle que soit la nature et la forme de l'onde incidente :

• il s'agit dans tous les cas d'exprimer que l'onde se propage dans un système fermé, c'est-à-dire se terminant par une condition aux limites,

• compte tenu de la linéarité de l'équation de propagation, l'onde résultante est la superposition des ondes existant dans la région considérée, à savoir l'onde progressive initiale et l'onde régressive qui prend naissance par réflexion sur la limite du système.

• la nature de cette condition aux limites permet d'exprimer la valeur de l'onde résultante sur la limite du système, et donc (connaissant la valeur de l'onde incidente sur la limite du système) d'en déduire la forme de l'onde réfléchie.

Considérons par exemple une onde incidente progressive représentée par la fonction \(F\), et soit \(G\) la fonction représentant l'onde réfléchie régressive.

Supposons que le système soit limité entre \(z=0\) et \(z=L\), et posons la condition aux limites suivante :

l'onde considérée a une amplitude nulle à l'extérieur du système (\(z<0\) ou \(z>L\)).

Cette condition aux limites signifie donc (par continuité) que l'onde totale (représentée par \(F+G\)) garde à tout instant une valeur nulle en \(z=0\) et en \(z=L\).

Supposons encore que la propagation de cette onde soit représentée par une translation en fonction du temps. On peut alors construire la translation de \(G\) symétrique de \(F\), satisfaisant les conditions aux limites :

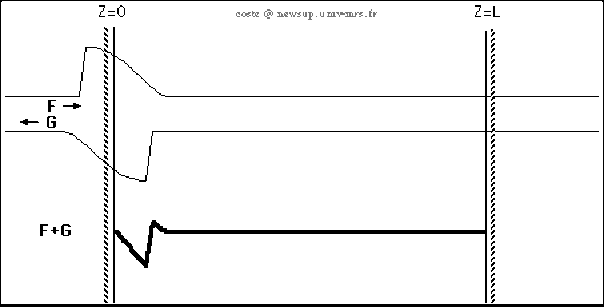
L'animation ci-dessus représente la propagation d'une onde progressive ainsi que la forme de l'onde régressive nécessaire obtenue par une réflexion telle que l'onde résultante satisfasse les conditions aux limites en \(z=L\).

Elle montre ensuite la propagation de l'onde résultante régressive, ainsi que la forme de l'onde progressive telle que l'onde résultante satisfasse les conditions aux limites en \(z=0\).