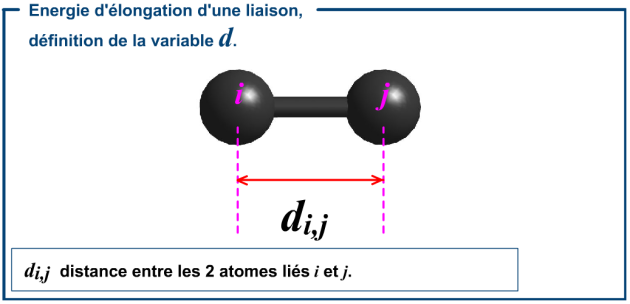
Energie d'élongation d'une liaison
L'énergie associée à l'élongation d'une liaison par rapport à sa distance d'équilibre est modélisée par une fonction quadratique.
Définition :
Pour une molécule la sommation porte sur toutes les liaisons de la molécule.
\(E_{Elongation}=\frac{1}{2}\displaystyle{\sum_{i}}K_{d,i}\left({d_{i}-d_{0,i}}\right)^{2}\) (Eq. 02)
\(d_{i}\) est la distance entre les atomes liés.
\(d_{0,i}\) est la distance d'équilibre standard pour la liaison \(i\).
\(K_{d,i}\) est la constante de force d'élongation de la liaison \(i\). Elle s'exprime en kJ.mol-1.\(\mathring{\textrm{A}}\) -2 (ou kcal.mol-1.\(\mathring{\textrm{A}}\) -2)
Ces paramètres (\(d_{0,i}\) et \(K_{d,i}\)) dépendent de la nature de la liaison et des atomes liés.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Exemple :
Pour une liaison simple entre deux carbones sp3 : \(d_{0}\) = 1,53 \(\mathring{\textrm{A}}\) et \(K_{d}\approx\) 610 kcal.mol-1.\(\mathring{\textrm{A}}\) -2
Pour une liaison double entre un carbone sp2 et un oxygène : \(d_{0}\) = 1,23 \(\mathring{\textrm{A}}\) et \(K_{d}\approx\) 1140 kcal.mol-1.\(\mathring{\textrm{A}}\) -2
La liaison Csp2=O a une distance d'équilibre plus petite (\(d_{0}\) = 1,23 \(\mathring{\textrm{A}}\) ) que la liaison Csp3-Csp3 (\(d_{0}\) = 1,53 \(\mathring{\textrm{A}}\) ) et son élongation (en compression ou extension) est plus coûteuse en énergie.
Cette expression n'est qu'une approximation de la variation d'énergie d'une liaison chimique en fonction de sa distance. Cette variation est mieux représentée par une courbe dite de Morse.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Au voisinage de la distance d'équilibre, la fonction quadratique constitue une bonne approximation locale de la courbe de Morse. Mais pour des distances plus courtes, la courbe de Morse monte en énergie beaucoup plus rapidement, tandis qu'au contraire, pour des distances plus grandes, la courbe de Morse tend vers une limite qui correspond à la dissociation de la liaison.
Dans certains champs de force, on introduit un terme cubique pour élargir quelque peu la zone de concordance entre la fonction ainsi calculée et la courbe de Morse. D'autres encore utilisent une fonction qui traduit mieux la forme de cette courbe :
\(E_{Elongation} = D_i \left( {1 - \alpha _i .\exp ^{(d_i - d_{i,0} )} } \right)^2 \) (Eq. 03)
ou
\(E_{Elongation} = D_i \left( {1 - \exp ^{ - \alpha _i .(d_i - d_{i,0} )} } \right)^2\)
qui nécessite la définition de trois paramètres \(D\), \(\alpha\) et \(d_0\) pour chaque type de liaison (\(D\) est la limite vers laquelle tends la fonction lorsque \(d\) augmente; \(\alpha\) caractérise la "courbure" de la fonction au voisinage de son minimum et \(d_0\) est la distance d'équilibre).
En pratique, ces raffinement compliquent les calculs et se révèlent peu utiles si on se limite à des géométries qui ne s'écartent pas trop de la distance d'équilibre standard des liaisons (déformations de l'ordre de 0,05 \(\mathring{\textrm{A}}\) ).