Les Orbitales Moléculaires

Afin de définir précisément les caractéristiques électroniques des atomes, nous avons besoin d'un jeu de fonctions permettant de définir le plus précisément possible les orbitales atomiques. Les fonctions hydrogénoïdes sont insufisantes dans le cas du traitement d'un système polyélectronique. Ci-dessous sont présentés deux types de solution assez communes utilisés pour représenter au mieux les Orbitales Atomiques.

Les orbitales de Slater

Les orbitales hydrogénoïdes sont les solutions de l'équation de Schrödinger appliquées à un système monoélectronique. L'étude d'un système comportant plusieurs électrons mène à l'introduction d'un potentiel coulombien répulsif électron-électron dans l'écriture de l'Hamiltonien complet, ce qui entraîne de considérables complications pour sa résolution. Afin de rendre cette résolution plus aisée, on applique une approximation considérant les électrons indépendamment les un des autres. Dès lors, l'Hamiltonien complet peut s'écrire comme la somme d'Hamiltoniens mono-électroniques et ses solutions sont alors le produit des orbitales hydrogénoïdes.

Ce type de solution ne tient pas compte de la répulsion électronique. Tenir en compte cette répulsion devrait mener à des orbitales plus diffuses, plus représentatives des solutions exactes. Une solution simple consiste alors à modifier la taille des solutions de type hydrogénoïde en modifiant l'attraction du noyau ressenti de la part de l'électron. Il s'agit alors de remplacer la valeur de la charge nucléaire Z apparaissant dans les expressions des orbitales hydrogénoïdes par une valeur qui refléterait au mieux la charge nucléaire ressentie par l'électron dans le cadre d'une perturbation moyenne apportée par les autres électrons. Cette charge Z* s'appelle la charge nucléaire effective ou encore la charge nucléaire apparente.

L'orbitale 1s orbitales s'écrit alors :

Une recherche de la valeur de Z* pour l'atome d'hélium (Z=2) mène alors à une valeur corrigée de 1,69. Ceci signifie que chacun des électrons de cette orbitale 1s se trouve dans le champ d'un atome de charge nucléaire +1,69 u.a. L'électron étant moins attiré par le noyau, l'orbitale est plus diffuse. Dans le cadre de cette approximation, les trois nombres quantiques n, l et m jouent toujours le même rôle.

Afin de simplifier encore la forme des solutions, J.C. Slater a défini de nouvelles formes analytiques pour les parties radiales qui ne dépendent que de n, et deviennent ainsi indépendantes du nombre quantique l.

Les parties radiales s'écrivent alors sous la forme :

Le paramètre \(\zeta\)vaut alors Z*/n. Le niveau énergétique associé à cette orbitale vaut quant à lui :

D'une façon générale, les orbitales de Slater s'écrivent sous la forme :

Ces orbitales sont regroupées sous l'acronyme STO, pour Slater Type Orbital.

Quelques limitations peuvent être notées concernant ces orbitales. Premièrement, elles ne présentent pas de nœuds dans leur partie radiale. De plus le calcul des intégrales biélectroniques à 3 ou 4 centres ne peut se faire de façon analytique.

Les orbitales gaussiennes

D'une façon générales, les orbitales gaussiennes s'écriront sous la forme :

Ces fonctions qui montrent une dépendance en r² sont d'un maniement beaucoup plus simple car le produit de deux gaussiennes est encore une fonction gaussienne, ce qui n'est pas le cas des orbitales de Slater. De plus, cette formulation en r² facilite grandement l'intégration des intégrales électroniques.

Malgré tout, cette dépendance en r2 entraîne une moins bonne représentation du comportement électronique dans les zones de proximité avec le noyau ou dans des zones où ils sont éloignés.

Elles seront employées préférentiellement aux orbitales de Slater.

Comme il est possible assez facilement de combiner cette fonction gaussienne, plusieurs solutions sont possibles pour représenter les orbitales atomiques.

1 - On peut en rester à une base minimale dans laquelle chaque orbitale atomique sera représentée par une GTO (Gaussian Type Orbital). Ainsi, nous ne retiendrons qu'une fonction de type s pour représenter l'orbitale 1s de l'hydrogène. Ce choix est loin d'être le meilleur du fait de la mauvaise représentation de la densité électronique à proximité et à grande distance du noyau.

2 – définir des orbitales de type double ou triple zéta. Il s'agit ici de doubler (ou de tripler) le nombre de fonction initiale pour représenter les orbitales atomique. Ainsi, l'orbitale 1s de l'atome d'hydrogène sera représenté par deux fonctions gaussiennes possédant des valeurs de zéta différentes. Cette augmentation des fonctions permet de mieux représenter la densité électronique à courte et longue distance.

3 – combiner linéairement les fonctions gaussiennes initiales (que l'on appellera les primitives : PGTO). Ces nouvelles fonctions sont définies alors comme des fonctions gaussiennes contractées (CGTO)

Quelques exemples de bases classiquement utilisées :

- STO-3G : 3 primitives gaussiennes vont être utilisées pour décrire une orbitale de type Slater. On pourrait utiliser plus de primitives mais le calcul serait plus long sans pour autant augmenter fortement la précision des résultats.

- 3-21G, 4-31G, 6-31G : il s'agit là de base dénommée à valence splittée (« split valence ») où seules les orbitales de valence seront doublées, triplées... Les chiffres 3, 4 et 6 avant le – correspondent au nombre de primitives gaussiennes qui seront utilisées pour décrire les orbitales de cœur des atomes lourds (autres que l'hydrogène). Les chiffres 21 et 31 avant la lettre G correspondent au nombre de fonction de bases qui seront utilisées pour décrire les orbitales de valence ; il s'agit ici de double zéta : deux chiffres indiquant deux fonctions, un 311G indiquerait une base triple zéta.

Exemple du jeu de base 3-21G : les orbitales de cœurs sont représentées par une contraction de 3 primitives gaussiennes, les orbitales de valence sont représentées par un base double zéta où l'une des orbitales découle de la contraction de deux gaussiennes et l'autre est une gaussienne simple.

Deux autres type de fonction sont classiquement ajoutées à ces bases, qui permettent notamment une meilleure représentation des hétéroatomes ou des systèmes chargés ou radicalaires :

- Fonction de polarisation : le but de ces orbitales est de décrire une modification de la forme de la densité électronique autour d'un noyau. Pratiquement, il s'agit de modifier la forme des orbitales atomiques. Pour cela, il suffit d'ajouter des orbitales de type p aux atomes d'hydrogène, des orbitales de type d au carbone...

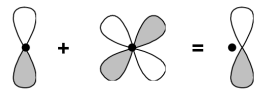
Le schéma simplifié ci-dessous explique succinctement la procédure qui permettrait de polariser les orbitales p de valence d'un atome de carbone par ajout d'une orbitale d

Pratiquement, à la base considéré, nous rajouterons une * pour indiquer l'ajout des ces orbitales de polarisation :

Par exemple:

6-31G* : ajout d'une orbitale d pour les éléments de la deuxième ligne et d'une orbitale f pour les métaux de transition

6-31G** : de même que ci-dessus plus ajout d'une orbitale de type p pour les atomes d'hydrogène.

- Fonction diffuse : le but de ces orbitales est de décrire une modification de la densité électronique à longue distance du noyau. Ceci est particulièrement vrai pour les atomes chargés ou radicalaire pour lesquels ces électrons sont généralement localisés dans des orbitales plus diffuses. Pratiquement, il s'agit d'ajouter une fonction avec un plus petit exponentiel permettant une « extinction » moins rapide de la fonction. Pour cela, il suffit d'ajouter à l'orbitale considérer un orbitale de même type mais de n (nombre quantique principal) plus grand.

Le schéma ci-dessous montre comment obtenir une orbitale s plus diffuse :

Pratiquement, à la base considérée, nous rajouterons un + pour indiquer l'ajout des ces orbitales diffuses :

Par exemple:

6-31+G : orbitales diffuses ajoutées sur les atomes lourds.

6-31++G : ajout supplémentaires sur les atomes d'hydrogène

De nombreuses autres bases existent et peuvent être utilisées dans des cas bien spécifiques. Nous n'en ferons pas la description ici.