L'élément de volume en coordonnées sphériques
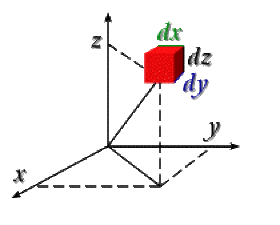
Dans le système cartésien, le volume élémentaire est :
\(\textrm d\tau=\mathrm{dx.dy.dz}\)
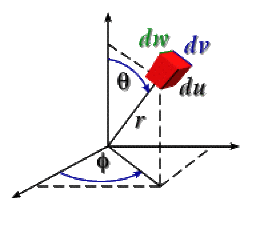
Dans le système sphérique où \(\mathrm{du}\), \(\mathrm{dv}\) et \(\mathrm{dw}\) sont les déplacements élémentaires suivant respectivement l'axe radial, la latitude et la longitude, il vaut :
\(\mathrm{dV=\textrm du. dv. dw}\)
Lors de l'intégration volumique, il est important de bien avoir à l'esprit que l'élément de volume dépend du système de coordonnées.
Cet élément de volume est défini comme un parallélépipède dont les arêtes mesurent les déplacements élémentaires obtenus lorsque l'on fait varier une seule des trois variables. Ainsi, dans le système cartésien, ces déplacements élémentaires sont respectivement \(\textrm dx\), \(\textrm dy\) et \(\textrm dz\). Dans le système de coordonnées sphériques, les choses sont plus subtiles.
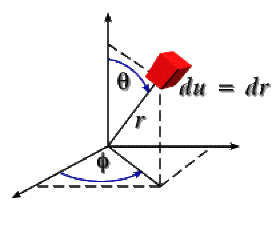
La variation du rayon \(\mathrm{r}\) conduit à un déplacement élémentaire :
\(\textrm{du}=\textrm{dr}\)
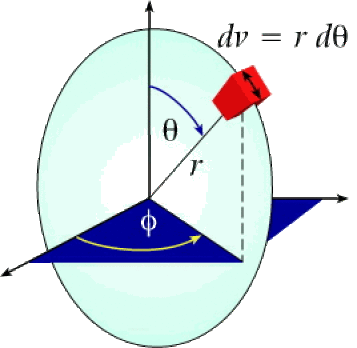
\(\mathrm{r}\) et l'angle de rotation \(\varphi\) étant fixes, la variation de l'angle d'écartement \(\theta\) fait circuler le point M sur un cercle de rayon \(\mathrm{r}\) (comme si M se déplaçait sur un méridien). Le déplacement correspond donc à une abscisse curviligne :
\(\textrm v=\textrm r.\theta\)
Le déplacement élémentaire correspondant est donc :
\(\textrm{dv}=\textrm r~\textrm d\theta\)
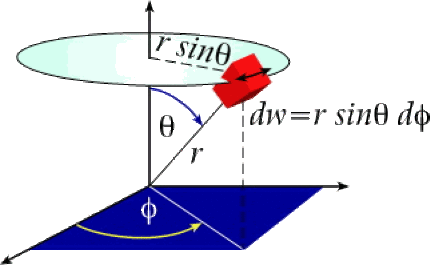
De même, la variation de l'angle de rotation \(\phi\) fait circuler M sur un cercle de rayon \(\mathrm{r}.\sin\theta\). Le déplacement élémentaire correspondant est :
\(\textrm{dw}=\textrm r.\sin\theta.\textrm d\phi\)
Le volume élémentaire devient donc :
\(\mathbf{\textrm dV=\textrm du.\textrm dv.\textrm dw=r^2.\sin\theta.\textrm dr.\textrm d\theta.\textrm d\phi}\)
Il faut noter que \(\textrm{dV}\) dépend de \(\mathrm{r}\) et de l'angle d'écartement \(\theta\) et n'est donc pas constant.
Ce volume élémentaire n'est pas le même dans les deux systèmes de coordonnées. On remarque notamment que le volume élémentaire en coordonnées sphériques augmente avec la distance à l'origine et il est nul sur l'axe \(\textrm{Oz}\) (quand l'angle \(\theta\) vaut 0 ou \(\pi\)).