Fonctions périodiques
On considère une fonction réelle dont on note \(D\) l'ensemble de définition.
Définition : Fonction périodique
On dit que \(f\) est périodique s'il existe un réel \(\mathcal T\in R^*\) tel que :
\(\displaystyle{\forall x\in\mathbb R,(x\in D\Leftrightarrow x+\mathcal T\in D)}\)
\(\displaystyle{\forall x\in D,f(x+\mathcal T)=f(x)}\).
On dit que \(\mathcal T\) est une période de \(f\) et que \(f\) est \(\mathcal T\)-périodique.
Une conséquence immédiate de la définition est que si \(f\) est \(\mathcal T\)-périodique alors -\(\mathcal T\) est aussi une période de \(f\).
Exemple :
a. Une fonction constante sur \(\mathbb R\) est périodique ; tout réel non nul en est une période.
Vous pouvez visualiser les points de la courbe représentant la fonction sur la figure suivante. Pour cela vous devez d'abord cliquer sur le bouton "Déplacer" puis déplacer le point à l'aide des flèches droite et gauche du clavier.
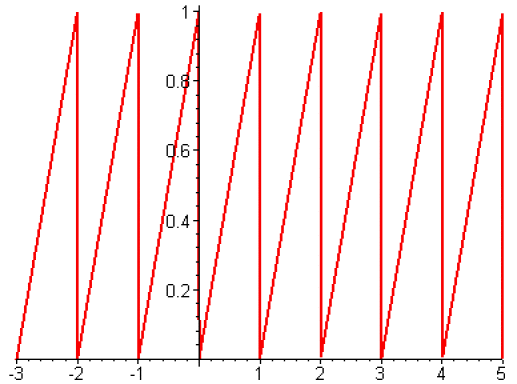
b. La fonction \(x\mapsto x-[x]\)est périodique, 1 est une période ainsi que tout entier non nul.
On conviendra désormais, pour une fonction périodique \(f\), de considérer également \(0\) comme une période de \(f\).
Proposition :
Si \(f\) est périodique et si \(\mathcal T \textrm{ et }\mathcal T'\) sont des périodes de \(f\), alors \(\mathcal T+\mathcal T'\) est une période de \(f\).
Preuve :
Cela repose sur la définition.
On note \(T\) l'ensemble des périodes de \(f\). Cet ensemble n'est, par hypothèse, pas vide puisque \(\mathcal T\) appartient à \(T\).
Soit \(x\in D\), on a alors successivement
\(x+\mathcal T\in D\textrm{ et }x +\mathcal T+\mathcal T '\in D\).
On en déduit \(f (x +\mathcal T+\mathcal T ')= f (x + \mathcal T)= f(x)\).
\(\mathcal T+\mathcal T '\) est donc une période de \(f\). En particulier pour tout \(n\in\mathbb Z\) on a \(n\mathcal T\in T\).
Si l'ensemble des périodes strictement positives de \(f\) a un plus petit élément strictement positif, soit \(\mathcal T_0\) cet élément est appelé période fondamentale de \(f\) .
Propriété :
Toutes les périodes de \(f\) sont de la forme \(n\mathcal T_0\) avec \(n\in\mathbb Z\).
Preuve :
Elle repose sur la division euclidienne d'une période \(\mathcal T\) par la période fondamentale \(\mathcal T_0\) .
Soit \(\mathcal T\) une période, que l'on supposera strictement positive, de \(f\); la division euclidienne de \(\mathcal T\) par \(\mathcal T_0\) conduit à l'égalité : \(\mathcal T =k\mathcal T_0+r \textrm{ avec }0\leq r<\mathcal T_0\).
Si \(r\) est strictement positif, c'est une période strictement positive, inférieure strictement à \(\mathcal T_0\) , ce qui est impossible. On a donc \(r=0 \textrm{ et }\mathcal T =n\mathcal T_0\).
Ainsi les fonctions sinus et cosinus ont pour période fondamentale \(2\pi\) et la fonction tangente \(\pi\). On désignera souvent par période la période fondamentale. Il peut se faire que \(T\) n'ait pas de plus petit élément strictement positif, c'est le cas pour la fonction caractéristique des rationnels : dans ce cas tout rationnel est période.
Quelques exercices
a. Montrer que la fonction \(\displaystyle{x\mapsto x-E[x]}\) est périodique de période 1.
Solution :
Soit \(f : \displaystyle{x\mapsto x-E[x]}\). Soit \(x\) un nombre réel. On note \(k\) sa partie entière, \(E[x]=k\), c'est-à-dire que \(k\) est l'unique nombre entier tel que \(k \leq x < k+1\). Alors l'entier \(n=k+1\) vérifie \(n \leq x+1 < n+1\), de sorte que \(n=E[x+1]\). Il s'ensuit que \(E[x+1]=n=k+1=E[x]+1\).
On a donc : \(f(x+1)=(x+1)-E[x+1]=(x+1)-(E[x]+1)=x-E[x]=f(x)\).
L'application \(f\) est donc périodique de période 1.

b. Quelle est la période de la fonction \(\displaystyle{x\mapsto\cos(4x+5)}\)?
Solution :
La solution est \(\displaystyle{\frac{\pi}{2}}\).
c. Trouver une fonction de période \(\frac{3}{4}\).
Solution :
Une fonction est \(\displaystyle{x\mapsto\sin\left(\frac{8\pi}{3}x\right)}\).
d. Montrer que, si la fonction \(f\) est \(\mathcal T\)-périodique et si on note \(\mathcal C_\mathcal T\) le graphe de la restriction de \(f\) à un intervalle semi-ouvert de longueur \(\mathcal T\), alors le graphe de \(f\) est la réunion de \(\mathcal C_\mathcal T\) et des translatés de \(\mathcal C_\mathcal T\) par les translations de vecteurs de composantes \((n\mathcal T,0),(n\in\mathbb Z)\).
Solution :
On note \(I\) un intervalle semi-ouvert de longueur \(\mathcal T\). Il s'agit alors d'une conséquence de la propriété suivante :
quel que soit le réel \(x_1\) il existe un réel \(x\) unique et un entier relatif \(n\) unique tel que :
\(x\in I \textrm{ et }x_1=x +n\mathcal T\textrm{ d'où }f(x_1)=f(x )\).
Si \(M\) est le point de coordonnées \((x, f(x))\) et \(N\) le point de coordonnées \((x_1, f(x_1))\) dans le repère orthonormé \((0,\vec i,\vec j)\) du plan , on a alors \(\displaystyle{\overrightarrow{MN}}=n\mathcal T\vec i\). D'où le résultat. Il suffit donc d'étudier \(f\) sur un intervalle semi-ouvert de longueur \(\mathcal T\).
Remarque :
Soit \(f\) une fonction telle qu'il existe \(\mathcal T\in\mathbb R_+^*\textrm{ et }\alpha\in\mathbb R\) vérifiant
\(\displaystyle{\forall x\in\mathbb R,(x\in D\Leftrightarrow x+\mathcal T\in D}\) \(\underline{et}\) \(\displaystyle{f(x+\mathcal T)=f(x)+\alpha)}\)
alors le graphe de \(f\) est invariant par les translations de vecteur \((n\mathcal T, n\alpha)\).
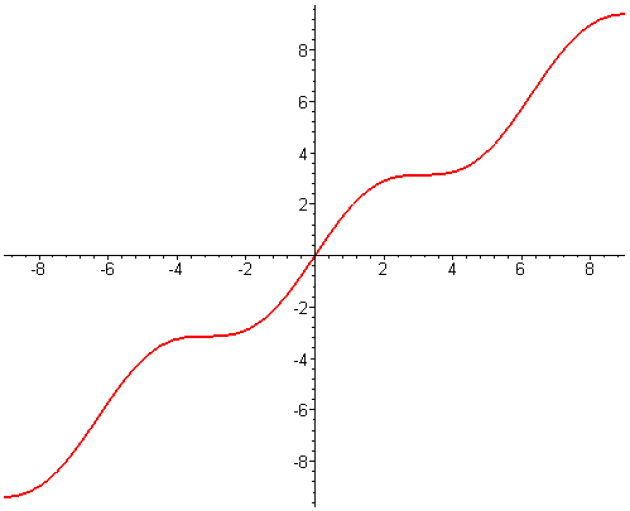
Exemple :
Considérons la fonction \(f :x\mapsto x+\sin x\) le graphe de \(f\) s'obtient à partir de sa restriction à l'intervalle \([-\pi,\pi[\) à l'aide de translations de vecteurs de composantes \((2n\pi,2n\pi), n\in\mathbb Z\).