Fonctions usuelles et leurs réciproques

Le plan \(P\) est orienté. Soit \(C\) le cercle de centre \(O\) et de rayon \(1,\) orienté dans le sens direct et muni d'un point origine \(I\) et soit \((O,\overrightarrow{i}, \overrightarrow{j})\) le repère orthonormé direct tel que \(\overrightarrow{i} = \overrightarrow{OI}.\)

A tout réel \(x\) est associé un point \(M\) unique de \(C,\) ce point \(M\) étant l'image du réel \(x\) par la surjection \(\rho\) de \(R\) sur \(C\) définie précédemment. Dans la suite, \(M\) sera appelé plus simplement le point image du réel \(x\) sur \(C.\)

Soient \(P\) et \(Q\) les projections orthogonales de \(M\) respectivement sur \((O, \overrightarrow{i})\) et \((O, \overrightarrow{j}).\) Alors, par définition,

\(\boxed{\cos{x} = \overline{OP}}\) \(\boxed{\sin{x} = \overline{OQ}}\)

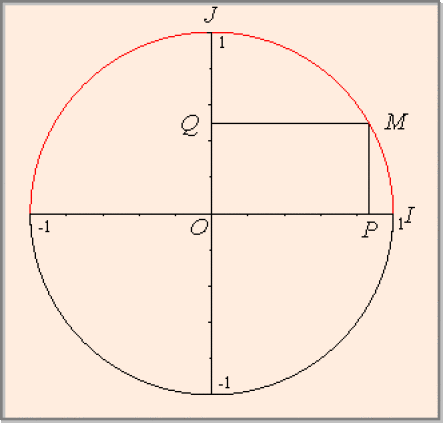
On définit ainsi deux fonctions de \(\mathbb R\) dans \(\mathbb R,\) \(x\mapsto \cos{x}~\textrm{et}~x\mapsto \sin{x}\) appelées respectivement fonction cosinus et fonction sinus.

Ces fonctions sont périodiques de période \(2\pi.\)

En effet soit \(x\) un réel et \(M\) son image sur \(C,\) tous les réels de la forme \(x+2k\pi,~k \in \mathbb Z\) ont le même point image \(M\) donc \(\forall k \in \mathbb Z~~\cos{(x+2k\pi)} = \cos{x},\) \(\sin{(x+2k\pi)} = \sin{x}.\)