Fonction tangente
On cherche pour quelles valeurs de \(x\) l'expression \(\frac{\sin{x}}{\cos{x}}\)est définie.
Pour tout réel \(x,~\cos{x} = 0 \Leftrightarrow x = \frac{\pi}{2} + k\pi,~k \in \mathbb Z\)
Explication :
Soient \(x\) un réel et \(M\) son image sur \(C\) et \(P\) la projection orthogonale de \(M\) sur \((O, \overrightarrow{i}).\)
\(\cos{x} = \overline{OP}\)
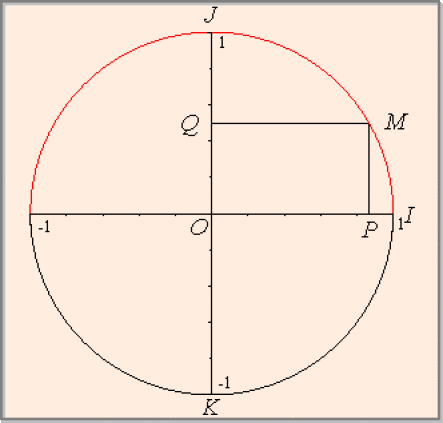
\(\cos{x}\) est nul si et seulement si l'image de \(x\) est le point \(J\) ou \(K,\) c'est-à-dire si et seulement si il existe \(k\) appartenant à \(\mathbb Z\) tel que ou \(x = \frac{\pi}{2} + 2k\pi\) ou \(x=3\frac{\pi}{2} + 2k\pi.\)
L'expression \(\frac{\sin{x}}{\cos{x}}\) est donc définie sur \(\mathbb R - \{\frac{\pi}{2} + k\pi, k \in \mathbb Z \}.\)
Définition :
On appelle fonction tangente, la fonction définie sur \(\mathbb R - \{\frac{\pi}{2} + k\pi, k \in \mathbb Z \}\)qui associe à tout réel \(x\) différent de \(\frac{\pi}{2} + k\pi\)le réel \(\frac{\sin{x}}{\cos{x}},\) noté \(\tan{x}.\)
Interprétation géométrique
Soit \(M\) l'image du réel \(x\) sur le cercle \(C\) de centre \(O\) et de rayon \(1,\) \(P\) la projection orthogonale de \(M\) sur \((O, \overrightarrow{i})\)et \(T\) l'intersection de la droite \((OM)\) avec l'axe \((I, \overrightarrow{j}).\) Le théorème de Thalès permet d'écrire :
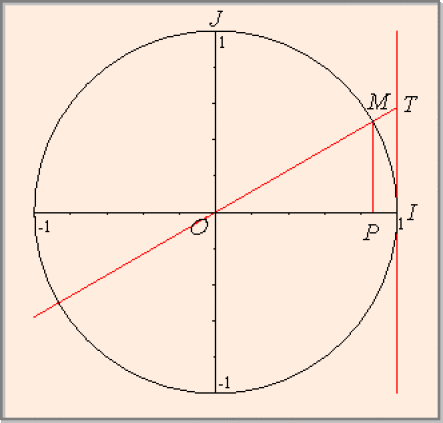
\(\frac{\overline{IT}}{\overline{PM}} = \frac{\overline{OI}}{\overline{OP}}\) or \(\overline{PM} = \sin{x},\) \(\overline{OI} = 1\) et \(\overline{OP} = \cos{x}\) d'où \(\overline{IT} = \frac{\sin{x}}{\cos{x}} = \tan{x}.\)
La droite \((OJ)\) est parallèle à la droite \((I, \overrightarrow{j}).\)
Donc lorsque \(M\) est en \(J\) (ce qui correspond à \(x=\frac{\pi}{2}+2k\pi,~k\in \mathbb Z),\) le point \(T\) n'existe pas. Cela correspond bien au fait que la fonction tangente n'est pas définie sur \(\{ \frac{\pi}{2} +k\pi,~k\in \mathbb Z\}.\)
Attention :
Cette ressource n'utilise que la définition géométrique des fonctions sinus et cosinus.
Définition : une autre définition des fonctions cosinus et sinus utilisant la notion de série
Quand la théorie des séries de fonctions est connue, on définit la fonction cosinus (respectivement sinus) comme la somme de la série entière de terme général \((-1)^n\frac{x^{2n}}{(2n)!}~\textrm{(resp.}~(-1)^n\frac{x^{2n+1}}{(2n+1) !}).\)
Pour tout réel \(x,\) \(\cos{x} = \displaystyle \lim_{n \rightarrow +\infty} (1 - \frac{x^2}{2!} + \frac{x^4}{4!} + \dots + (-1)^n\frac{x^{2n}}{(2n)!})\)
Pour tout réel \(x,\) \(\sin{x} = \displaystyle \lim_{n \rightarrow +\infty}(x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots + (-1)^n\frac{x^{2n+1}}{(2n+1)!})\)
Les propriétés des fonctions sinus et cosinus sont alors démontrées à partir des propriétés des séries de fonctions.