Introduction
Résultat préliminaire
\(\boxed{\forall x \in ]-\frac{\pi}{2}, \frac{\pi}{2}[~~~~|\sin x| \leq |x|}\)
Justification géométrique
Le plan orienté est rapporté à un repère orthonormé \((O, \overrightarrow{i}, \overrightarrow{j}).\) Soit \(C\) le cercle de centre \(O\) et de rayon \(1.\) Soit \(x\) un réel de l'intervalle \(]0, \frac{\pi}{2}[,\) \(M\) le point de coordonnées \((\cos x, \sin x),\) \(P\) le projeté orthogonal de \(M\) sur \((O, \overrightarrow{i})\) et \(A\) le point de coordonnées \((1, 0).\)
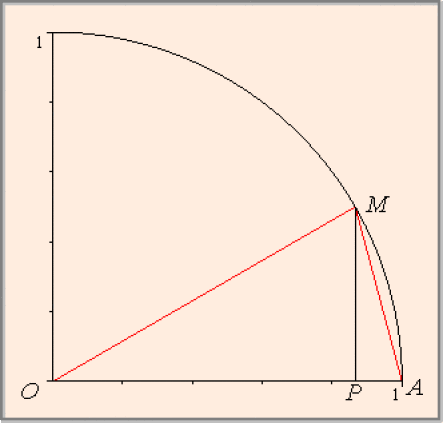
L'aire du triangle \(OAM\) est égale à \(\frac{1}{2}PM \times OA\)donc est égale à \(\frac{1}{2}\sin x,\) l'aire du secteur angulaire \(OAM\) est proportionnelle à la longueur de l'arc \(\overset{\frown}{AM}\)donc est égale à \(\pi \times \frac{x}{2\pi}.\)
En comparant ces deux aires on peut donc écrire \(\forall x \in ]0, \frac{\pi}{2}[~~~~\frac{1}{2}\sin x \leq \frac{1}{2}x\) soit \(\forall x \in ]0, \frac{\pi}{2}[~~~~\sin x \leq x\)
Cette inégalité est encore vraie pour \(x= 0\)et comme la fonction sinus est impaire,
\(\forall x \in ]-\frac{\pi}{2}, \frac{\pi}{2}[~~~~|\sin x| \leq |x|\)
On a donc aussi \(\boxed{\forall x \in \mathbb R~~~~|\sin x| \leq |x|}\)car \(\forall x\in \mathbb R~~~~-1 \leq \sin x \leq 1\) et si \(x\notin ]-\frac{\pi}{2}, \frac{\pi}{2}[~~~~|x| > 1.\)