Dérivabilité
Théorème :
Les fonctions sinus, cosinus et tangente sont dérivables sur leur ensemble de définition.
\(\forall x \in \mathbb R~~~~(\cos)'(x) = -\sin x\)
\(\forall x \in \mathbb R~~~~(\sin)'(x) = \cos x\)
\(\forall x \in \mathbb R - \{\frac{\pi}{2} + k\pi , k \in \mathbb Z\}~~~~(\tan)'(x) = 1+\tan^2 x = \frac{1}{\cos^2x}\)
Démonstration :
Première étape : justification géométrique de \(\displaystyle \lim_{x \rightarrow 0}\frac{\sin x}{x} = 1\)
Le plan orienté est rapporté à un repère orthonormé \((O, \overrightarrow{i}, \overrightarrow{j}).\) Soit \(C\) le cercle de centre \(O\) et de rayon \(1.\) Soit \(x\) un réel de l'intervalle \(]0, \frac{\pi}{2}[,\) \(M\) le point de coordonnées \((\cos x, \sin x),\) \(A\) le point de coordonnées \((1, 0)\)et \(T\) le point d'intersection de la droite \((OM)\) et de la tangente en \(A\) au cercle \(C.\)
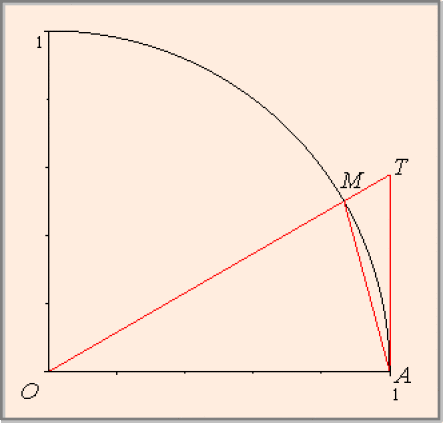
En comparant les aires du triangle \(OAM,\) du secteur angulaire \(OAM\) et du triangle \(OAT,\) on peut écrire : \(\forall x \in ]0, \frac{\pi}{2}[~~~~\frac{1}{2}\sin x \leq \frac{1}{2}x \leq \frac{1}{2}\tan x\)
et en divisant les trois membres par \(\frac{1}{2}\sin x\)(qui est strictement positif)
on a : \(\forall x \in ]0, \frac{\pi}{2}[~~~~1\leq \frac{x}{\sin x} \leq \frac{1}{\cos x}\)
puis en passant aux inverses (ces trois réels étant strictement positifs) \(\forall x \in ]0, \frac{\pi}{2}[~~~~\cos x \leq \frac{\sin x}{x} \leq 1.\)
On en déduit \(\displaystyle \lim_{x \rightarrow 0, x > 0}\frac{\sin x}{x} = 1.\)
La fonction \(x \mapsto \frac{\sin x}{x}\) étant paire, on a aussi \(\displaystyle \lim_{x \rightarrow 0, x < 0}\frac{\sin x}{x} = 1\) d'où \(\displaystyle \lim_{x \rightarrow 0}\frac{\sin x}{x} = 1.\)
Cette limite exprime la dérivabilité de la fonction sinus en \(0,\) sa dérivée valant \(1\) en ce point.
Deuxième étape : dérivabilité de cosinus en \(0.\)
Pour \(x \neq 0~~~~\frac{\cos x - \cos 0}{x} = \frac{\cos x - 1}{x} = \frac{-2\sin^2\frac{x}{2}}{x} = -\frac{\sin\frac{x}{2}}{\frac{x}{2}}\times \sin\frac{x}{2}\)
(utilisation de la formule \(\sin^2a = \frac{1-\cos 2a}{2})\)
\(\displaystyle \lim_{x \rightarrow 0}\frac{x}{2} = 0\)donc \(\displaystyle \lim_{x \rightarrow 0}\frac{\sin \frac{x}{2}}{\frac{x}{2}} = 1,\) de plus \(\displaystyle \lim_{x \rightarrow 0} \sin \frac{x}{2} = 0\) d'où \(\displaystyle \lim_{x \rightarrow 0}\frac{\cos x - 1}{x} = 0\)
La fonction cosinus est donc dérivable en \(0,\) sa dérivée valant \(0\) en ce point.
Troisième étape : dérivabilité de sinus en un point quelconque \(x_0.\)
Pour \(h \neq 0,\)
\(\frac{\sin(x_0 + h) - \sin x_0}{h} = \frac{\sin x_0 \cos h + \cos x_0 \sin h - \sin x_0}{h} = \sin x_0 \frac{(\cos h - 1)}{h} + \cos x_0 \frac{\sin h}{h}\)
\(\displaystyle \lim_{h \rightarrow 0}\frac{\cos h - 1}{h} = 0\)et \(\displaystyle \lim_{h \rightarrow 0} \frac{\sin h}{h} = 1\)d'où \(\displaystyle \lim_{h \rightarrow 0}\frac{\sin(x_0+h) - \sin x_0}{h} = \cos x_0.\)
La fonction sinus est donc dérivable en \(x_0,\) sa dérivée valant en ce point \(\cos x_0.\)
La démonstration pour la dérivabilité de la fonction cosinus est analogue.
La fonction tangente est le quotient de deux fonctions dérivables sur \(\mathbb R.\) Elle est donc dérivable sur son ensemble de définition \(D,\) et pour tout réel \(x\) de \(D.\)
\((\tan)'(x) = \frac{\sin' x\cos x - \sin x \cos' x}{\cos^2 x} = \frac{\cos^2x + \sin^2x}{\cos^2x} = 1 + \tan^2x = \frac{1}{\cos^2x}\)