Fonctions usuelles et leurs réciproques

La fonction th est continue et strictement croissante de \(\mathbb R\) sur \(]-1, +1[.\) Elle établit une bijection de \(\mathbb R\) sur \(]-1, +1[.\)

Elle admet donc une fonction réciproque appelée argument tangente hyperbolique et notée Argth, qui est continue, strictement croissante et dérivable sur \(]-1, +1[,\) car la dérivée de th ne s'annule pas sur \(\mathbb R.\) On a donc :

\(\begin{cases}y = \textrm{Argth}x\\x \in ]-1,+1[\end{cases}\Leftrightarrow\begin{cases}\textrm{th}y=x\\y \in \mathbb R\end{cases}\)

En appliquant le théorème général des fonctions réciproques :

\(\forall x \in]-1,+1[~~\textrm{Argth}'x=\frac{1}{\textrm{th}'(\textrm{Argth}x)}=\frac{1}{1-\textrm{th}^2(\textrm{Argth}x)}\)

et \(\textrm{th}(\textrm{Argth}x)=x.\)

\(\forall x \in ]-1,+1[,~~\textrm{Argth}'x=\frac{1}{1-x^2}\)

\(y = \textrm{Argth}x \Leftrightarrow x=\textrm{th}y=\frac{e^{2y}-1}{e^{2y}+1} \Leftrightarrow(e^{2y}+1)x=e^{2y}-1\\\Leftrightarrow e^{2y}(1-x) = 1+x\Leftrightarrow e^{2y}=\frac{1+x}{1-x}\)

d'où \(2y = \ln(\frac{1+x}{1-x})\)et il vient

\(\forall x \in ]-1,+1[,~~\textrm{Argth}x=\frac{1}{2}\ln(\frac{1+x}{1-x})\)

\(\color{blue} x\mapsto\textrm{Argth}x\)

\(\color{green}x\mapsto \textrm{th}x\)

\(\color{red} x\mapsto x\)

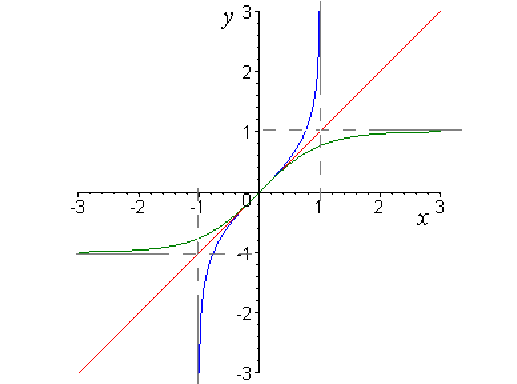
Par lecture des graphes, on retrouve que le graphe de Argth est le symétrique de celui de th par rapport à la droite d'équation \(y = x.\)

Le graphe de th ayant des asymptotes horizontales, le graphe de Argth a des asymptotes verticales.