Fonctions usuelles et leurs réciproques

1.a (1pt) Pour pouvoir calculer le nombre \(\frac{\ln x}{x},\) le réel \(x\) doit appartenir au domaine de définition de la fonction \(\ln\) et ne pas être nul (existence de \(\frac{1}{x}),\) d'où \(\color{blue} \mathbb I = ]0,+\infty[.\)

1.b (3pt ) Etant un quotient de fonctions continues et dérivables sur \(\mathbb I,\) \(f\) est continue et dérivable sur \(\mathbb I\)

et \(\forall x \in \mathbb I~~f'(x)=\frac{\frac{1}{x}x-\ln x}{x^2}=\frac{1-\ln x}{x^2}.\)

2.a Étude à la borne \(0\) (1pt)

\(f(x)=\frac{1}{x}\ln x,~~\lim_{x\rightarrow0^+}\frac{1}{x}=+\infty,~~\lim_{x\rightarrow0^+}\ln x=-\infty,\) donc \(\color{blue}\lim_{x\rightarrow0^+}f(x)=-\infty\color{black}.\)

Étude à la borne \(+\infty\) (1pt)

D'après un résultat du cours \(\color{blue}\lim_{x\rightarrow+\infty}\frac{\ln x}{x} = 0\color{black}.\)

2.b \(\forall x \in \mathbb I~~f'(x)=\frac{1-\ln x}{x^2}\)donc la dérivée de \(f\) s'annule et change de signe au point \(e,\) on obtient le tableau de variations (2pt) :

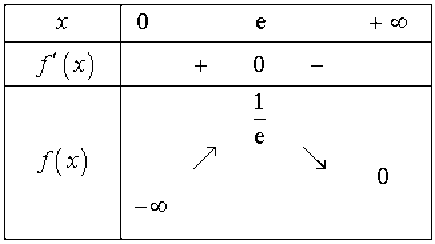
Représentation graphique (2pt)

\(\color{red}x\mapsto \frac{\ln x}{x}\)

\(\color{green}x\mapsto\frac{1}{e}\)

\(\color{blue}x = e\)

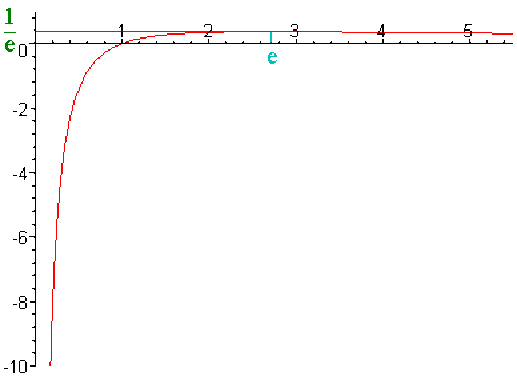
On observe que les droites \(x=0\)et \(y=0\)sont des asymptotes.

La fonction admet un maximum égal à \(\frac{1}{e},\) atteint au point \(e.\)

3. (5pt) \(\forall x > 0~~x^\alpha = e^x\Leftrightarrow e^{\alpha\ln x}=e^x\Leftrightarrow \alpha\ln x = x\) car l'exponentielle est bijective. Il est temps de commencer la discussion :

\(\color{red} 1^{\textrm{er}}~\textrm{cas}\) \(\alpha = 0\)

L'équation devient \(1=e^x,\) or \(\forall x > 0~~e^x>1\)donc \((E)\)n'a pas de solution.

Pour les autres cas : \(x~\textrm{solution de }~(E)\Leftrightarrow f(x)=\frac{1}{\alpha}.\)

D'après l'étude précédente \(f(]0,+\infty[)=]-\infty,\frac{1}{e}],\) ce qui amène quatre nouveaux cas, en utilisant le graphe et le tableau de variations.

\(\color{red} 2^{\textrm{ème}}~\textrm{cas}\) \(\alpha < 0\)

\(\frac{1}{\alpha}\in]-\infty, 0[,~~f(]0,1[)=]-\infty,0[,\) \(f\) est continue et strictement croissante sur \(]0,1[\)donc établit une bijection entre \(]0,1[\)et \(]-\infty,0[\)ainsi il existe un unique réel \(x_1\)vérifiant \(f(x_1)=\frac{1}{\alpha}\)donc \((E)\)admet une solution.

\(\color{red} 3^{\textrm{ème}}~\textrm{cas}\) \(0<\alpha < e\)

\(\frac{1}{\alpha} > \frac{1}{e}\) donc \((E)\)n'a pas de solution.

\(\color{red} 4^{\textrm{ème}}~\textrm{cas}\) \(\alpha = e\)

\((E)\)admet une solution.

\(\color{red} 5^{\textrm{ème}}~\textrm{cas}\) \(\alpha > e\)

\(\frac{1}{\alpha}\in]0,\frac{1}{e}[,~~f(]1,e[)=]0,\frac{1}{e}[=f(]e,+\infty[),\) \(f\) est continue et strictement croissante sur \(]1,e[\)donc établit une bijection entre \(]1,e[\)et \(]0,\frac{1}{e}[\)ainsi il existe un unique réel \(x_1,~~x_1\in]1, e[\)vérifiant \(f(x_1)=\frac{1}{\alpha}.\)

De même \(f\) est continue et strictement décroissante sur \(]e, +\infty[\)donc établit une bijection entre \(]e,+\infty[\)et \(]0,\frac{1}{e}[\)ainsi il existe un unique réel \(x_2,~~x_2\in]e,+\infty[\)vérifiant \(f(x_2)=\frac{1}{\alpha}.\) Donc \((E)\)admet deux solutions.

Conclusion :

\(\begin{array}{|c | c | c | c | c |}\hline \alpha < 0 & \alpha = 0 & 0<\alpha<e&\alpha=e&\alpha > e\\ 1~solution & 0~solution& 0~solution&1~solution&2~solutions \\\hline\end {array}\)