Matrice associée à la composée de deux applications linéaires
Soient\( E, \mathcal F\) et \(\mathcal G\) trois espaces vectoriels de type fini sur un même corps \(\mathbf K\). Soient \(\phi\) une application linéaire de\( E\) dans \(\mathcal F\) et \(\psi\) une application linéaire de \(\mathcal F\) dans \(\mathcal G\). Pour pouvoir considérer les matrices associées à \(\phi\) et \(\psi\) , il est nécessaire de choisir des bases sur \(E, \mathcal F \textrm{ et }\mathcal G\).
Soient donc \(p\) la dimension de \(E\) et\( \mathcal B_E=(e_1,e_2,\cdots,e_p)\) une base de \(E, n \)la dimension de\( \mathcal F\) et \(\mathcal B_F=(f_1,f_2,\cdots,f_n)\) une base de \(\mathcal F\) et enfin \(q\) la dimension de \(\mathcal G\) et \(\mathcal B_G=(g_1,g_2,\cdots,g_q)\) une base de \(\mathcal G\).
On est donc dans le schéma suivant :
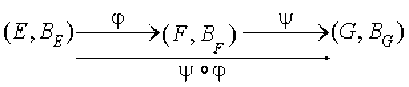
De manière naturelle, on cherche à déterminer la matrice associée à \(\psi\circ\phi\) par rapport aux bases \(\mathcal B_E \textrm{ et }\mathcal B_F\) de \(E\) et \(\mathcal G\) respectivement. On obtient le résultat suivant
Théorème : Matrice associée à la composée de deux applications linéaires
Soient \(E, \mathcal F\) et \(\mathcal G\) trois espaces vectoriels de type fini sur un même corps \(\mathbf K\), de dimension respectivement égale à \(p, n \textrm{ et }q\).
Soient \(\mathcal B_E=(e_1,e_2,\cdots,e_p)\) une base de \(E\), \(\mathcal B_F=(f_1,f_2,\cdots,f_n)\) une base de\( \mathcal F\) et \(\mathcal B_G=(g_1,g_2,\cdots,g_q)\) une base de \(\mathcal G\).
Soient \(\psi\) une application linéaire de \(E\) dans \(\mathcal F\) et \(\psi\) une application linéaire de\( \mathcal F\) dans \(\mathcal G\).
Alors on a :
\(\displaystyle{[\psi\circ\phi]_{\mathcal B_E}^{\mathcal B^G}=[\psi]_{\mathcal B_F}^{\mathcal B^G}[\phi]_{\mathcal B_E}^{\mathcal B^F}}\)
Commentaires
Autrement dit, à condition de bien choisir les bases, la matrice associée à la composition de deux applications linéaires est le produit des matrices associées à chacune d'elle, dans le même ordre.
Cela justifie, à posteriori, les conditions d'existence et la définition du produit des matrices.
En effet, pour que le produit \(\mathcal{BA}\) de deux matrices \(\mathcal A\) et \(\mathcal B\) ait un sens, il faut que le nombre de colonnes de la matrice \(\mathcal B\) soit égal au nombre de lignes de la matrice \(\mathcal A\).
Si, avec les notations introduites ci-dessus,\(\mathcal A=[\phi]_{\mathcal B_E}^{\mathcal B^F}\) et \(\mathcal B=[\psi]_{\mathcal B_F}^{\mathcal B^G}\) , cette condition est satisfaite, puisque le nombre de colonnes de \(\mathcal B\) est égal à la dimension de l'espace\( \mathcal F\) et qu'il en est de même pour le nombre de lignes de la matrice \(\mathcal A\).
Remarquons que l'hypothèse : " l'espace d'arrivée de \(\phi\) est égal à l'espace de départ de\( \psi\) " est une condition nécessaire et suffisante pour que la composée \(\psi\circ\phi\) existe.
Enfin la définition explicite du produit de deux matrices a été choisie pour avoir cette relation entre composée d'applications linéaires et produit de matrices.
Démonstration :
Un peu lourde quant aux notations, cette preuve est pourtant simple quant aux idées car elle est uniquement basée sur la définition de la matrice associée à une application linéaire par rapport à des bases choisies, et sur la définition du produit de deux matrices.
La première étape consiste à fixer les notations
Soit \(\mathcal A=[\phi]_{\mathcal B_E}^{\mathcal B^F}=(a_{i,j})_{\begin{array}{cccccc}1\leq i\leq n\\1\leq j\leq p\end{array}}\textrm{ et }\mathcal B=[\psi]_{\mathcal B_F}^{\mathcal B^G}=(b_{r,s})_{\begin{array}{cccccc}1\leq r\leq q\\1\leq s\leq n\end{array}} \)et , les coefficients \(a_{i,j}\) et \(b_{r,s}\) sont caractérisés par les égalités suivantes :
\(\displaystyle{\forall j,1\leq j\leq p,\quad\phi(e_j)=\sum_{i=1}^{i=n}a_{i,j}f_i}\)
\(\displaystyle{\forall s,1\leq s\leq n,\quad\psi(f_s)=\sum_{r=1}^{r=q}b_{r,s}g_r}\)
La deuxième étape consiste à chercher la matrice associée à \(\psi\circ\phi\) par rapport aux bases\( \mathcal B_E\) et \(\mathcal B_G\)
Il s'agit donc d'exprimer, pour tout \(j,1\leq j\leq p,\psi\circ\phi(e_j)\) dans la base
\(\mathcal B_G=(g_1,g_2,\cdots,g_q)\) car le terme de la \(r\)-ième ligne, \(j\)-ième colonne de la matrice cherchée est la coordonnée de \(\psi\circ\phi\) sur le vecteur \(g_r\) .
Les relations (1), implique :
\(\displaystyle{\psi\circ\psi(e_j)=\psi(\sum_{i=1}^{i=n}a_{i,j}f_i)=\sum_{i=1}^{i=n}a_{i,j}}\psi(f_i)\)
D'où, en utilisant les relations (2), on a pour tout \(j,1\leq j\leq p,\).
\(\displaystyle{\psi\circ\phi(e_j)=\sum_{i=1}^{i=n}a_{i,j}(\sum_{r=1}^{r=q}b_{r,i}g_r)}\)
Les propriétés des lois d'un espace vectoriel, permettent d'écrire :
\(\displaystyle{\psi\circ\phi(e_j)=\sum_{r=1}^{r=q}(\sum_{i=1}^{i=n}a_{i,j}b_{r,i})g_r}\)
Le coefficient de \(\psi\circ\phi(e_j)\) sur le vecteur \(g_r\) de la base \(\mathcal B_G=(g_1,g_2,\cdots,g_q)\) est donc égal à
\(\displaystyle{\sum^{i=n}_{i=1}a_{i,j}b_{r,i}=\sum^{i=n}_{i=1}b_{r,i}a_{i,j}}\)
(puisque les coefficients sont dans un corps commutatif).
On reconnaît là exactement le terme général de la matrice \(\mathcal BA\), ce qui achève la démonstration