Enchaîner des changements de bases
Partie
Question
Soit \(E\) un espace vectoriel de dimension n sur un corps \(K\), muni de trois bases
\(\mathcal B_1=(\epsilon_1,...,\epsilon_n),\mathcal B_2=(a_1,...,a_n),\mathcal B_3=(b_1,...,b_n)\).
On note les matrices de passage \(A=P_{\mathcal B_1,\mathcal B_2},B=P_{\mathcal B_1,\mathcal B_3},M=P_{\mathcal B_2,\mathcal B_3}\)
Exprimer la matrice \(M\) à l'aide des matrices \(A\) et \(B\).
Aide simple
Rappel du produit de matrices de passage \(P_{\mathcal B,\mathcal B''}=P_{\mathcal B,\mathcal B'}P_{\mathcal B',\mathcal B''}\)
Aide à la lecture
La matrice de passage de la base \(\mathcal B_1\) à la base est notée \(P_{\mathcal B_1,\mathcal B_2}\).
Solution détaillée
A partir du diagramme 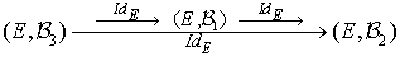
on a \([Id_E]^{\mathcal B_2}_{\mathcal B_3}=[Id_E]^{\mathcal B_2}_{\mathcal B_1}[Id_E]^{\mathcal B_1}_{\mathcal B_3}\) et \(P_{\mathcal B_2,\mathcal B_3}=P_{\mathcal B_2,\mathcal B_1}P_{\mathcal B_1,\mathcal B_3}\).
Or \(P_{\mathcal B_2,\mathcal B_1}=(P_{\mathcal B_1,\mathcal B_2})^{-1}=A^{-1}\), \(P_{\mathcal B_1,\mathcal B_3}=B\) d'où la relation \(M=A^{-1}B\).
Question
Montrer que les vecteurs \(e_1=(1,2,1),e_2=(2,3,3),e_3=(3,7,1)\) déterminent une base \(\mathcal B\) de l'espace vectoriel \(R^3\).
Montrer que les vecteurs \(e^\prime_1=(2,-3,1),e^\prime_2=(3,-1,5),e^\prime_3=(1,-4,3)\) déterminent une base \(\mathcal B^\prime\) de l'espace vectoriel \(R^3\).
Déterminer la matrice de passage de la base \(\mathcal B\) à la base \(\mathcal B^\prime\).
Aide méthodologique
3. appliquer le résultat de la première question en utilisant la base canonique de \(R^3\) comme intermédiaire.
Solution détaillée
La famille \(\{e_1,e_2,e_3\}\) contient 3 vecteurs et la dimension de \(R^3\) est égale à 3, donc il suffit de vérifier qu'elle est libre pour démontrer que \((e_1,e_2,e_3)\) est une base de \(R^3\).
Soit \(\lambda_1,\lambda_2,\lambda_3\) trois réels tels que \(\lambda_1e_1+\lambda_2e_2+\lambda_3e_3=0\) alors le triplet \((\lambda_1,\lambda_2,\lambda_3)\) est solution du système : \(\left\{\begin{array}{cccccc}\lambda_1+2\lambda_2+3\lambda_3=0&L_1\\2\lambda_1+3\lambda_2+7\lambda_3=0&L_2\\\lambda_1+3\lambda_2+\lambda_3=0&L_3\end{array}\right.\).
Ce système est équivalent à
\(\left\{\begin{array}{llllll}\lambda_1+2\lambda_2+3\lambda_3=0&L_1&\leftarrow&L_1\\-\lambda_2+\lambda_3=0&L_2&\leftarrow&L_2-2L_1\\\lambda_2-2\lambda_3=0&L_3&\leftarrow&L_3-L_1\end{array}\right.\Leftrightarrow\left\{\begin{array}{llllll}\lambda_1+2\lambda_2+3\lambda_3=0&L_1&\leftarrow&L_1\\-\lambda_2+\lambda_3=0&L_2&\leftarrow&L_2\\-\lambda_3=0&L_3&\leftarrow&L_3+L_2\end{array}\right.\)
donc l'unique solution est (0,0,0).
\(\mathcal B=(e_1,e_2,e_3)\) est une base de \(R^3\).
Par une démarche analogue, on est amené à résoudre le système
\(\left\{\begin{array}{cccccc}2\lambda_1+3\lambda_2+\lambda_3=0&L_1\\-3\lambda_1-\lambda_2-4\lambda_3=0&L_2\\\lambda_1+5\lambda_2+3\lambda_3=0&L_3\end{array}\right.\Leftrightarrow\left\{\begin{array}{cccccc}\lambda_1+5\lambda_2+3\lambda_3=0&L_1&\leftarrow&L_3\\14\lambda_2+5\lambda_3=0&L_2&\leftarrow&L_2+3L_3\\-7\lambda_2-5\lambda_3=0&L_3&\leftarrow&L_1-2L_3\end{array}\right.\)
Ce système est équivalent à
\(\left\{\begin{array}{llllll}\lambda_1+3\lambda_3+5\lambda_2=0&L_1\\5\lambda_3+14\lambda_2=0&L_2\\-5\lambda_3-7\lambda_2=0&L_3\end{array}\right.\Leftrightarrow\left\{\begin{array}{lllllll}\lambda_1+3\lambda_3+5\lambda_2=0&L_1&\\5\lambda_3+14\lambda_2=0&L_2&\\7\lambda_2=0&L_3&\leftarrow L_3+L_2\end{array}\right.\)
donc l'unique solution est (0,0,0).
\(\mathcal B^\prime=(e^\prime_1,e^\prime_2,e^\prime_3)\) est une base de \(R^3\).
Notons \(\mathcal B_0=(\epsilon_1,\epsilon_2,\epsilon_3)\), la base canonique de \(R^3\). Nous pouvons appliquer le résultat de la question 1. aux trois bases \(\mathcal B_0,\mathcal B,\mathcal B'\).
\(A=P_{\mathcal B_0,\mathcal B},B=P_{\mathcal B_0,\mathcal B'},M=P_{\mathcal B,\mathcal B'},M=A^{-1}B\)
Or \(A=\left(\begin{array}{c c c}1&2&3\\2&3&7\\1&3&1\end{array}\right)\), \(B=\left(\begin{array}{c c c}2&3&1\\-3&-1&-4\\1&5&3\end{array}\right)\)
Pour trouver la matrice \(A^{-1}\) on va exprimer les vecteurs de \(\mathcal B_0\) en fonction de ceux de \(\mathcal B\). Par définition
\(\left\{\begin{array}{lllllll}\epsilon_1+2\epsilon_2+\epsilon_3=e_1\\2\epsilon_1+3\epsilon_2+3\epsilon_3=e_2\\3\epsilon_1+7\epsilon_2+\epsilon_3=e_3\end{array}\right.\Rightarrow\left\{\begin{array}{lllllll}\epsilon_1+2\epsilon_2+\epsilon_3&=&e_1\\-\epsilon_2+\epsilon_3&=&-2e_1+e_2\\\epsilon_2-2\epsilon_3&=&-3e_1+e_3\end{array}\right.\Rightarrow\left\{\begin{array}{lllllll}\epsilon_1+2\epsilon_2+\epsilon_3&=&e_1\\-\epsilon_2+\epsilon_3&=&-2e_1+e_2\\-\epsilon_3&=&-5e_1+e_2+e_3\end{array}\right.\)
On obtient donc \(\epsilon_3=5e_1-e_2-e_3,\epsilon_2=7e_1-2e_2-e_3,\epsilon_1=-18e_1+5e_2+3e_3\)
d'où \(A^{-1}=\left(\begin{array}{c c c}-18&7&5\\5&-2&-1\\3&-1&-1\end{array}\right)\) or \(B=\left(\begin{array}{c c c}2&3&1\\-3&-1&-4\\1&5&3\end{array}\right)\)
donc \(M=\left(\begin{array}{c c c}-18&7&5\\5&-2&-1\\3&-1&-1\end{array}\right)\left(\begin{array}{c c c}2&3&1\\-3&-1&-4\\1&5&3\end{array}\right)=\left(\begin{array}{c c c}-52&-36&-31\\15&12&10\\8&5&4\end{array}\right)\)