Rang d'un produit de matrices
Partie
Soient \(A\) une matrice appartenant à \(M_{p,n}\), \(B\) une matrice appartenant à \(M_{nq}(R)\), \(f\) l'application linéaire de \(R^n\) dans \(R^p\) associée à la matrice \(A\) relativement aux bases canoniques \(B_n\) de \(R^n\) et \(B_p\) de \(R^p\), \(g\) l'application linéaire de \(R^q\) dans \(R^n\) associée à la matrice \(B\) relativement aux bases canoniques \(B_q\) de \(R^q\) et \(B_n\) de \(R^n\).
Question
Soit \(\{u_1,u_2,...,u_k\}\), \(1\le k\le{q}\),une famille de \(k\) vecteurs de \(R^q\).
On suppose que la famille \(\{f(g(u_1)),f(g(u_2)),...,f(g(u_k))\}\) est libre, montrer que la famille \(\{g(u_1),g(u_2),...,g(u_k)\}\) est libre.
En déduire que le rang du produit \(AB\) est inférieur ou égal au rang de \(B\).
Aide simple
Pour montrer une implication \((P\Rightarrow Q)\), il est plus simple ici de raisonner par contraposition, c'est-à-dire de démontrer l'implication équivalente \((\textrm{non}Q\Rightarrow\textrm{non}P)\).
La matrice \(AB\) est associée à l'application linéaire \(f \bigcirc g\).
Aide à la lecture
Si \(A\) appartient à \(M_{p,n}(R)\), et \(B\) appartient à \(M_{nq}(R)\), on peut faire le produit de \(A\) et de \(B\) et la matrice \(AB\) appartient à \(M_{p,q}(R)\).
A toute matrice réelle \(M\) de type \((m, n)\) on peut associer une application linéaire \(\phi\) de \(R^n\) dans \(R^m\) telle que la matrice associée à \(\phi\) dans des bases données soit \(M\).
Aide méthodologique
Le rang d'une matrice est égal au rang de ses vecteurs colonnes, c'est aussi le rang d'une application linéaire qui lui est associée.
La méthode suggérée par le texte est celle qui fait intervenir les applications linéaires associées.
Solution détaillée
1. On est dans la situation suivante :
\(\begin{array}{cccccc}f:R^n\rightarrow R^p&/&A=M(f,B_n,B_p)\\g:R^q\rightarrow R^n&/&B=M(g,B_q,B_n)\end{array}\)
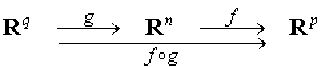
Soit \(\{u_1,u_2,...,u_k\}\), \(1\le k\le{q}\),une famille de \(k\) vecteurs de \(R^q\).
Si la famille \(\{g(u_1),g(u_2),...,g(u_k)\}\) est liée, alors il existe un \(k\)-uplet non nul \((\alpha_1,\alpha_2,...,\alpha_k)\) de \(R^k\), tel que \(\alpha_1g(u_1)+\alpha_2g(u_2)+...+\alpha_kg(u_k)=0\).
Comme \(f\) est une application linéaire on en déduit :
\(\begin{array}{cccccc}\alpha_1f(g(u_1))+\alpha_2f(g(u_2))+...+\alpha_kf(g(u_k))&=&f(\alpha_1g(u_1)+\alpha_2g(u_2)+...+\alpha_kg(u_k))\\&=&f(0)\\&=&0\end{array}\)
Donc la famille \(\{f(g(u_1)),f(g(u_2)),...,f(g(u_k))\}\) est liée.
On a donc démontré l'implication \((\{g(u_1),g(u_2),...,g(u_k)\}\textrm{li\'ee}\Rightarrow(\{f(g(u_1)),f(g(u_2)),...,f(g(u_k))\}\textrm{li\'ee}\)
O a donc l'implication équivalente suivante (la contraposée) : \((\{f(g(u_1)),f(g(u_2)),...,f(g(u_k))\}\textrm{libre})\Rightarrow(\{g(u_1),g(u_2),...,g(u_k)\}\textrm{libre})\).
2. Soit \(r\) le rang de la matrice \(AB\).
Comme \(A\) est une matrice à \(p\) lignes et \(n\) colonnes et \(B\) une matrice à \(n\) lignes et \(q\) colonnes, la matrice \(AB\) a \(p\) lignes et \(q\) colonnes.
L'entier \(r\) est donc le rang de ces \(q\) colonnes.
La matrice \(AB\) est la matrice de \(f\bigcirc g\) relativement aux bases canoniques \(B_q\) de \(R^q\) et \(B_p\) de \(R^p\). Si \(B_q=(e_1,e_2,...,e_q)\), les colonnes de \(AB\) sont formées par les coordonnées des vecteurs \(f(g(e_i)),1\le i\le{q}\).
Donc le rang de \(AB\) est égal au rang des vecteurs \(f(g(e_i)),1\le i\le{q}\).
Ce rang étant le nombre maximum de vecteurs linéairement indépendants de la famille \(\{f(g(e_1)),f(g(e_2)),...,f(g(e_q))\}\) notons \(e^\prime_1,e^\prime_2,...,e^\prime_r\) \(r\) vecteurs de la base \(B_q\), tels que la famille \(\{f(g(e^\prime_1)),f(g(e^\prime_2)),...,f(g(e^\prime_r)\}\) soit libre.
D'après 1., cela entraîne que la famille \(\{g(e^\prime_1),g(e^\prime_2),...,g(e^\prime_r)\}\) est libre. Or cette famille de \(r\) vecteurs est contenue dans la famille \(\{g(e_1),g(e_2),...,g(e_q)\}\) , donc \(r\) est inférieur ou égal au rang de \(g\).
Comme le rang de \(g\) est égal au rang de \(B\), on a bien : le rang de \(AB\) est inférieur ou égal au rang de \(B\).
Question
Montrer que le rang du produit \(AB\) est aussi inférieur ou égal au rang de \(A\).
Aide simple
Pour montrer une implication \((P\Rightarrow Q)\), il est plus simple ici de raisonner par contraposition, c'est-à-dire de démontrer l'implication équivalente \((\textrm{non}Q\Rightarrow\textrm{non}P)\).
La matrice \(AB\) est associée à l'application linéaire \(f \bigcirc g\).
Aide à la lecture
Si \(A\) appartient à \(M_{p,n}(R)\), et \(B\) appartient à \(M_{nq}(R)\), on peut faire le produit de \(A\) et de \(B\) et la matrice \(AB\) appartient à \(M_{p,q}(R)\).
A toute matrice réelle \(M\) de type \((m, n)\) on peut associer une application linéaire \(\phi\) de \(R^n\) dans \(R^m\) telle que la matrice associée à \(\phi\) dans des bases données soit \(M\).
Aide méthodologique
Le rang d'une matrice est égal au rang de ses vecteurs colonnes, c'est aussi le rang d'une application linéaire qui lui est associée.
La méthode suggérée par le texte est celle qui fait intervenir les applications linéaires associées.
Solution détaillée
Puisque \(g(R^q)\) est contenu dans \(R^n\), \(f(g(R^q))\) est contenu dans \(f(R^n)\), autrement dit : \(\mathrm{Im}(f\bigcirc g)\subset\mathrm{Im}f\) donc \(\mathrm{dim}\mathrm{Im}(f\bigcirc g)\le\mathrm{dim}\mathrm{Im}f\).
Or \(\mathrm{dim}\mathrm{Im}(f\bigcirc g)=\mathrm{rang}(f\bigcirc g)=\mathrm{rang}(AB)\) et \(\mathrm{dim}\mathrm{Im}f=\mathrm{rang}(f)=\mathrm{rang}(A)\). Donc le rang de \(AB\) est inférieur ou égal au rang de \(A\).