Exercice n°1
Partie
Question
On considère les fonctions :
\(\displaystyle{g_1 : x\rightarrow\frac{x^5-2x+1}{x^3+3x+1}}\)
\(\displaystyle{g_2 : x\rightarrow\frac{x^4+1}{x^2+5x+1}}\)
\(\displaystyle{g_3 : x\rightarrow\frac{x^4+2x^3+1}{x^3+3x+1}}\)
\(\displaystyle{g_4 : x\rightarrow\frac{x^4+1}{x^3+3x^2+x+1}}\)
\(\displaystyle{g_5 : x\rightarrow\frac{x^6+2x^2+1}{x^3+3x+1}}\)
\(\displaystyle{g_6 : x\rightarrow\frac{x^5+1}{x^3+3x^2+x+1}}\)
\(\displaystyle{g_7 : x\rightarrow\frac{x^6+x^5+x+1}{x^5-3x+1}}\)
\(\displaystyle{g_8 : x\rightarrow\frac{x^4+2x^2+1}{x^3+x^2+1}}\)
Ces fonctions sont définies au voisinage de l’infini (quand \(x\) tend vers \(\pm1\)). Sans aucun calcul, groupez ces fonctions en familles suivant la nature de leur branches infinies.
Rappel de cours
Voyons comment les développements limités permettent de préciser l'allure locale du graphe d'une fonction, en particulier en donnant une tangente, et la position du graphe par rapport à cette tangente.
Considérons une fonction \(f\) définie au voisinage d'un \(x_0\in\mathbb R\). On a vu qu'il est équivalent de dire que \(f\) (ou son prolongement en \(x_0\)) est dérivable en \(x_0\) ou de dire que \(f\) admet un développement limité à l'ordre 1 (au moins). Nous supposerons cette condition réalisée, et nous noterons \(a_0=f(x_0)\) et \(a_1=f'(x_0)\).
On sait que le graphe \(\Gamma\) de \(f\) admet alors une tangente \(\Delta\) en \(x_0\), d'équation \(y=a_0+a_1(x-x_0)\).
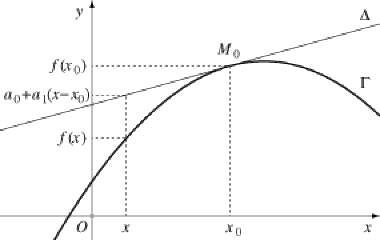
Supposons de plus qu'il existe un entier \(p\ge2\) tel que \(f\) admette un développement limité à l'ordre \(p\), de la forme
f(x)=a_0+a_1(x-x_0)+a_p(x-x_0)^p+(x-x_0)^p\epsilon(x) avec \(a_p\ne0\),
c'est-à-dire que tous les cœfficients \(a_k\) sont nuls pour \(1<k<p\), et \(a_p\) non nul ; on dit que c'est le premier développement limité significatif de \(f\).
Alors le signe de \(a_p\) donne la position de \(\Gamma\) par rapport à la droite \(\Delta\).
Pour le voir, il suffit d'écrire le développement limité précédent sous la forme
\(f(x)-y=(x-x_0)^p(a_p+\epsilon(x))\).
Vu que \(\displaystyle{\lim_{x\rightarrow x_0}\epsilon(x)=0}\), le signe de la parenthèse \((a_p+\epsilon(x))\) est au voisinage de \(x_0\) le même que celui de \(a_p\) (il suffit d'utiliser la définition de la limite).
D'autre part, le signe de \((x - x_0)^p\) est :
positif si \(p\) est pair ;
positif pour \(x>x_0\) et négatif pour \(x<x_0\) si \(p\) est impair.
Ainsi, on connaît localement le signe de \(f(x)-y\), c'est-à-dire la position locale du graphe de \(f\) par rapport à la tangente \(\Delta\) :
quand \(f(x)-y>0\), \(\Gamma\) est au dessus de \(\Delta\);
quand \(f(x)-y<0\), \(\Gamma\) est au dessous de \(\Delta\).
Solution détaillée
On peut trouver les trois familles suivantes suivant la différence des degrés des numérateurs et des dénominateurs :
Courbes dont le graphe présente une parabole asymptote : \(g_1, g_2, g_6\)
Courbes dont le graphe présente une asymptote : \(g_3, g_4, g_7, g_8\)
Courbes dont le graphe présente une branche parabolique sans parabole asymptote \(g_5\)