Exercice n°2
Partie
Question
On considère les fonctions :
\(\displaystyle{g_1 :x\rightarrow\frac{x^5-2x+1}{x^3+3x+1}}\)
\(\displaystyle{g_2 : x\rightarrow\frac{x^4+1}{x^2+5x+1}}\)
\(\displaystyle{g_5 :x\rightarrow\frac{x^6+2x^2+1}{x^3+3x+1}}\)
\(\displaystyle{g_6 :x\rightarrow\frac{x^5+1}{x^3+3x^2+x+1}}\)
Calculez un développement généralisé avec assez de termes pour connaître la position de la courbe par rapport à sa parabole asymptote éventuelle. Tracez les toutes sur un même graphe.
Rappel de cours
Voyons comment les développements limités permettent de préciser l'allure locale du graphe d'une fonction, en particulier en donnant une tangente, et la position du graphe par rapport à cette tangente.
Considérons une fonction \(f\) définie au voisinage d'un \(x_0\in\mathbb R\). On a vu qu'il est équivalent de dire que \(f\) (ou son prolongement en \(x_0\)) est dérivable en \(x_0\) ou de dire que \(f\) admet un développement limité à l'ordre 1 (au moins). Nous supposerons cette condition réalisée, et nous noterons \(a_0=f(x_0)\) et \(a_1=f'(x_0)\).
On sait que le graphe \(\Gamma\) de \(f\) admet alors une tangente \(\Delta\) en \(x_0\), d'équation \(y=a_0+a_1(x-x_0)\).
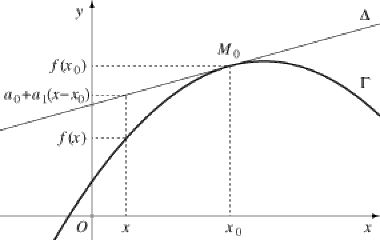
Supposons de plus qu'il existe un entier \(p\ge2\) tel que \(f\) admette un développement limité à l'ordre \(p\), de la forme
f(x)=a_0+a_1(x-x_0)+a_p(x-x_0)^p+(x-x_0)^p\epsilon(x) avec \(a_p\ne0\),
c'est-à-dire que tous les cœfficients \(a_k\) sont nuls pour \(1<k<p\), et \(a_p\) non nul ; on dit que c'est le premier développement limité significatif de \(f\).
Alors le signe de \(a_p\) donne la position de \(\Gamma\) par rapport à la droite \(\Delta\).
Pour le voir, il suffit d'écrire le développement limité précédent sous la forme
\(f(x)-y=(x-x_0)^p(a_p+\epsilon(x))\).
Vu que \(\displaystyle{\lim_{x\rightarrow x_0}\epsilon(x)=0}\), le signe de la parenthèse \((a_p+\epsilon(x))\) est au voisinage de \(x_0\) le même que celui de \(a_p\) (il suffit d'utiliser la définition de la limite).
D'autre part, le signe de \((x - x_0)^p\) est :
positif si \(p\) est pair ;
positif pour \(x>x_0\) et négatif pour \(x<x_0\) si \(p\) est impair.
Ainsi, on connaît localement le signe de \(f(x)-y\), c'est-à-dire la position locale du graphe de \(f\) par rapport à la tangente \(\Delta\) :
quand \(f(x)-y>0\), \(\Gamma\) est au dessus de \(\Delta\);
quand \(f(x)-y<0\), \(\Gamma\) est au dessous de \(\Delta\).
Solution détaillée
\(\displaystyle{g_1 : =x^2-3-\frac{1}{x}+\frac{1}{x}\epsilon\left(\frac{1}{x}\right)}\)
\(\displaystyle{g_2 : =x^2-5x+24-115\frac{1}{x}+\frac{1}{x}\epsilon\left(\frac{1}{x}\right)}\)
\(\displaystyle{g_5 : =x^3-3x-1+11\frac{1}{x}+\frac{1}{x}\epsilon\left(\frac{1}{x}\right)}\)
\(\displaystyle{g_6 : =x^2-3x+8-22\frac{1}{x}+\frac{1}{x}\epsilon\left(\frac{1}{x}\right)}\)
Commentaire :
On constate que :
\(g_1\) a une parabole aymptote d’équation \(y=x^2-3\). La différence entre les deux courbes est de signe opposé à \(x\) (signe du terme \(\displaystyle{-\frac{1}{x}}\)). Cela veut dire que la courbe est au dessus de la parabole asymptote quand \(x\) tend vers \(-\infty\) et en dessous quand \(x\) tend vers \(+\infty\).
\(g_2\) a une parabole asymptote d’équation \(y=x^2-5x+24\) et une étude analogue montre que que la courbe est au dessus de la parabole asymptote quand \(x\) tend vers \(-\infty\) et en dessous quand \(x\) tend vers \(+\infty\).
\(g_6\) a aussi une parabole asymptote d’équation \(y=x^2-3x+8\), avec le même type de position entre courbe et parabole.
Par contre la courbe \(g_5\) a une branche parabolique dans la direction de l’axe \(Oy\) et n’a pas de parabole asymptote. Mais on peut remarquer que \(g_5\) a une cubique asymptote d’équation \(y=x^3-3x-1\), c’est à dire que la différence entre un point de la courbe associée à \(g_5\) et cette cubique tend vers \(0\) quand \(x\) tend vers l’infini.
De plus cette différence est du signe de \(\displaystyle{11*\frac{1}{x}}\).
Quelle est la signification de ces propriétés ?
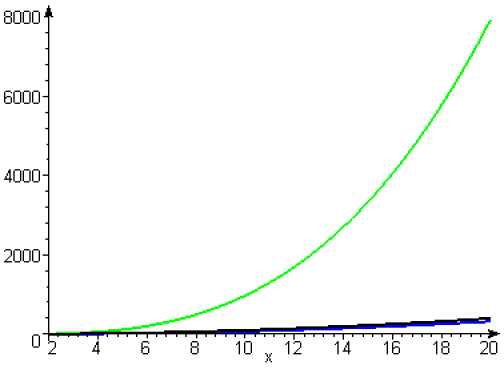
On a tracé sur un même graphe ces quatre fonctions à l’aide d’un logiciel de calcul formel, pour \(x\) variant entre 2 et 20. Les fonctions sont tracées \(g_1(x)\) en noir, \(g_2(x)\) en bleu, \(g_5(x)\) en vert, \(g_6(x)\) en jaune. Sur le graphe seuls apparaissent une courbe en vert ayant une branche parabolique dans la direction de l’axe \(Oy\) et une courbe en bleu, avec des valeurs de \(y\) faibles. Pourquoi ? Quelle est la signification de ces tracés ? La seule courbe qui apparait est en fait celle qui s’appoche de la cubique. L’ordre de grandeur de \(x^3\) est beaucoup plus grand que \(x^2\). Donc avec une même échelle déterminée par les valeurs de \(g_5\), les autres courbes n’apparaissent pas nettement.
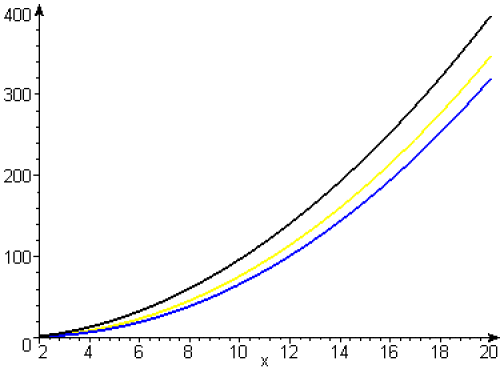
Pour faire apparaitre les autres courbes, on représente seulement le tracé des fonctions \(g_1(x)\) en noir, \(g_2(x)\) en bleu, \(g_6(x)\) en jaune. On voit alors nettement que ces courbes ressemblent à des paraboles et on vérifie leurs positions respectives.