Séries de fonctions

La série de fonctions \(\left( \sum{\frac{1}{2^{n}}} \cos{(12^{n} \pi x)}\right)\) converge uniformément sur \(\mathbb{R}\) (facile, convergence normale).

Posons \(f(x) = \overset{+\infty}{\underset{n=0}{\sum}}~\frac{1}{2^{n}} \cos{(12^{n} \pi x)}\). f est continue sur \(\mathbb{R}\) (convergence uniforme d'une série de fonctions continues sur \(\mathbb{R}\)).

Montrons que \(f\) n'est dérivable nulle part.

Soit \(x \in \mathbb{R}\),

pour \(p \in \mathbb{N}\), posons \(\alpha_{p}(x) = \frac{f \left( x + \frac{1}{12^{p}} \right) - f(x)}{\frac{1}{12^{p}}} = 12^{p} \left[ f \left( x + \frac{1}{12^{p}} \right) -f(x) \right]\) et \(\beta_{p}(x) = \frac{f \left( x + \frac{1}{2. 12^{p}} \right) - f(x)}{\frac{1}{2.12^{p}}} = 2.12^{p} \left[ f \left( x + \frac{1}{2.12^{p}} \right) - f(x) \right]\).

Si \(f\) était dérivable en \(x\), on aurait \(\underset{p \rightarrow +\infty}{\textrm{lim}} \alpha_{p}(x) = f'(x)\) et \(\underset{p \rightarrow +\infty}{\textrm{lim}} \beta_{p}(x) = f'(x)\), donc les ensembles \(\{\alpha_{p}(x ), p \in \mathbb{N}\}\) et \(\{\beta_{p}(x ), p \in \mathbb{N}\}\) seraient bornés.

Si l'on prouve que \(\underset{p \in \mathbb{N}}{\textrm{max}}\bigg\{|\alpha_{p}(x)|,|\beta_{p}(x)|\bigg\}=+\infty\), on aurait alors une contradiction, et \(f\) ne serait donc pas dérivable en \(x\).

Nous allons donc essayer de montrer que \(\underset{p \in \mathbb{N}}{\textrm{max}}\bigg\{|\alpha_{p}(x)|,|\beta_{p}(x)|\bigg\}=+\infty\).

\(\begin{array}{r c l}\alpha_{p}(x)&=&12^{p} \left[ f \left( x + \frac{1}{12^{p}} \right) -f(x) \right]\\ \\&=&12^{p} \left[\overset{+\infty}{\underset{n=0}{\sum}}~\frac{1}{2^{n}} \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{12^{p}}\right)} - \overset{+\infty}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\cos{(12^{n} \pi x)}\right]\\ \\ &=&12^{p} \left[ \overset{+\infty}{\underset{n=0}{\sum}}~\frac{1}{2^{n}} \left[ \cos{ \left( 12^{n} \pi x + \frac{12^{n} \pi}{12^{p}} \right) } - \cos{(12^{n} \pi x)} \right] \right]\end{array}\)

Or, pour \(n > p\), \(\frac{12^{n} \pi}{12^{p}} = 0~\textrm{mod}~2\pi\), donc \(\cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{12^{p}}\right)} = \cos{(12^{n} \pi x)}\); on en déduit :

\(\begin{array}{r c l}\alpha_{p}(x) & = & 12^{p} \left[ \overset{p}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left[\cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{12^{p}}\right)} - \cos{(12^{n} \pi x)} \right] \right] \\ \\& = & 12^{p} \left[ \frac{1}{2^{p}}~\left[\cos{\left( 12^{p} \pi x + \frac{12^{p} \pi}{12^{p}}\right)} - \cos{(12^{p} \pi x)} \right] + \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left[\cos{\left( 12^{n} x + \frac{12^{n} \pi}{12^{p}}\right)} - \cos{(12^{n} \pi x)} \right] \right] \\ \\& = & 12^{p} \left[ \frac{-2 \cos{(12^{p} \pi x)}}{2^{p}} + \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left[\cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{12^{p}}\right)} - \cos{(12^{n} \pi x)} \right] \right] \\\end{array}\)

\(\begin{array}{r c l}|\alpha_{p}(x)| & = & 12^{p} \left|\underset{A}{\underbrace{ \frac{-2 \cos{(12^{p} \pi x)}}{2^{p}}}} + \underset{B}{\underbrace{\overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}} \left[ \cos{(12^{n} \pi x + \frac{12^{n} \pi}{12^{p}})} - \cos{(12^{n} \pi x)} \right] }} \right|\end{array}\)

Or, \(|A + B| \geq |A| - |B|\) pour tout \(A\) et \(B\) réels ; on en déduit :

\(\begin{array}{r c l}|\alpha_{p}(x)| & \geq & 12^{p} \left[ \left| \frac{-2 \cos{(12^{p} \pi x)}}{2^{p}} \right| - \left| \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left[ \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{12^{p}} \right)} - \cos{(12^{n} \pi x)} \right] \right| \right] \\ \\& \geq & 6^{p} \left| 2\cos{(12^{p} \pi x)} \right| - 12^{p} \left| \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left[ \cos{(12^{n} \pi x + \frac{12^{n} \pi}{12^{p}})} - \cos{(12^{n} \pi x)} \right] \right|\end{array}\)

De plus, \(\left| \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}} \left[ \cos{(12^{n} \pi x + \frac{12^{n} \pi}{12^{p}})} - \cos{(12^{n} \pi x)} \right] \right| \leq \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left| \cos{(12^{n} \pi x + \frac{12^{n} \pi}{12^{p}})} - \cos{(12^{n} \pi x)} \right|\).

Or, pour tout \(u\) de \(v\) de \(\mathbb{R}\), \(| \cos{(u)} - \cos{(v)} | \leq |u - v|\) ; ceci se démontre en écrivant :

\(\begin{array}{r c l}\cos{(u)} - \cos{(v)} & = & -2 \sin{(\frac{u - v}{2})} \sin{(\frac{u + v}{2})} \\ \\|\cos{(u)} - \cos{(v)}| & = & 2 \left| \sin{(\frac{u - v}{2})} \right| . \left| \sin{(\frac{u + v}{2})} \right| \\ \\|\cos{(u)} - \cos{(v)}| & \leq & 2 \left| \sin{(\frac{u - v}{2})} \right| \qquad \textrm{car} \left| \sin{(\frac{u + v}{2})} \right| \leq 1 \\ \\& \leq & 2\left|\frac{u-v}{2}\right| \qquad \textrm{car} |\sin{(t)}| \leq |t| \\ \\& \leq & |u - v|\end{array}\)

Donc :

\(\begin{array}{r c l}\left| \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left[\cos{(12^{n} \pi x + \frac{12^{n} \pi}{12^{p}})} - \cos{(12^{n} \pi x)} \right] \right| & \leq & \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left|12^{n} \pi x + \frac{12^{n} \pi}{12^{p}} - 12^{n} \pi x \right| \\ \\& \leq & \overset{p-1}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left| \frac{12^{n} \pi}{12^{p}} \right| \\ \\& \leq & \frac{\pi}{12^{p}}~\overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}}.12^{n} \\ \\& \leq & \frac{\pi}{12^{p}}~\overset{p-1}{\underset{n=0}{\sum}} 6^{n} \\ \\& = & \frac{\pi}{12^{p}}~.~\frac{1 - 6^{p}}{1 - 6} \\ \\& = & \frac{(6^{p} -1) \pi}{5~.~12^{p}} \\ \\& \leq & \frac{6^{p} \pi}{5~.~12^{p}} \\ \\& = & \frac{\pi}{5~.~2^{p}}\\ \\\end{array}\)

Il vient alors : \(|\alpha_{p}(x)| \geq 6^{p} |2 \cos{(12^{p} \pi x)}| - 12^{p} \frac{\pi}{5~.~2{p}} = 6^{p} \left[ |2 \cos{(12^{p} \pi x)}| - \frac{\pi}{5} \right]\)

\(|\alpha_{p}(x)| \geq 6^{p} \left[ |2\cos{(12^{p} \pi x)}| - \frac{\pi}{5}\right]\)

Procédons de la même manière pour \(|\beta_{p}(x)|\) :

\(\begin{array}{r c l}\beta_{p}(x) & = & 2 . 12^{p}\left[ f\left( x + \frac{1}{2 . 12^{p}} \right) -f(x)\right] \\ \\ & = & 2 . 12^{p} \left[ \overset{+\infty}{\underset{n = 0}{\sum}}~\frac{1}{2^{n}}~\cos{\left(12^{n} \pi x + \frac{12^{n} \pi}{2 . 12^{p}}\right)} - \overset{+\infty}{\underset{n=0}{\sum}}~\frac{1}{2n}~\cos{(12^{n} \pi x)} \right] \\ \\ &=&2.12^{p} \left[ \overset{+\infty}{\underset{n=0}{\sum}}~\frac{1}{2^{n}}~\left[\cos{(12^{n} \pi x + \frac{12^{n} \pi}{2 . 12^{p}})} - \cos{(12^{n} \pi x)} \right]\right]\end{array}\)

Or, pour \(n > p\), \(\frac{12^{n} \pi}{2 . 12^{p}} = 0~\textrm{mod}~2 \pi\), donc \(\cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{2 . 12^{p}}\right)} = \cos{(12^{n} \pi x )}\); on en déduit :

\(\begin{array}{r c l} \beta_{p}(x) & = & 2.12^{p} \left[ \overset{p}{\underset{n = 0}{\sum}}~\frac{1}{2^{n}} \left[ \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}} - \cos{(12^{n} \pi x)} \right) } \right] \right] \\ \\& = & 2.12^{p} \left[ \frac{1}{2^{p}} \left[ \cos{\left( 12^{p} \pi x + \frac{12^{p} \pi}{2.12^{p}} - \cos{(12^{p} \pi x)} \right) } \right] + \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left[ \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}} - \cos{(12^{n} \pi x)} \right) }\right]\right] \\ \\& = & 2.12^{p} \left[ \frac{-\sin{(12^{p} \pi x)} - \cos{(12^{p} \pi x)}}{2^{p}} + \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left[ \cos{(12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}})} - \cos{(12^{n} \pi x)} \right]\right] \\ \\& = & 2.12^{p} \left| \underset{A}{\underbrace{\frac{-\sin{(12^{p} \pi x)} - \cos{(12^{p} \pi x)}}{2^{p}}}} + \underset{B}{\underbrace{ \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left[ \cos{\left(12^{n} + \frac{12^{n} \pi}{2.12^{p}}\right)} - \cos{(12^{n} \pi x)} \right]}} \right|\end{array}\)

Or, \(|A + B| \geq |A| - |B|\) pour tout \(A\) et \(B\) réels ; on en déduit : 

\(\begin{array}{r c l}|\beta_{p}(x)| & \geq & 2.12^{p} \left[ \left| \frac{-\sin{(12^{p} \pi x)} - \cos{(12^{p} \pi x)}}{2^{p}} \right| - \left| \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left[ \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}}\right)} - \cos{(12^{n} \pi x)}\right] \right| \right] \\& \geq & 2.6^{p} \left|\sin{(12^{p} \pi x)} + \cos{(12^{p} \pi x)}\right| - 2.12^{p} \left| \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left[ \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}}\right)} - \cos{(12^{n} \pi x)} \right] \right| \\\end{array}\)

Ainsi, \(|\sin{(12^{p} \pi x)} + \cos{(12^{p} \pi x)}| = \left|\sqrt{2} \cos{\left( 12^{p} \pi x - \frac{\pi}{4}\right)}\right|\)

De plus, \(\Bigg| \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left[ \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}}\right)} - \cos{(12^{n} \pi x)} \right] \Bigg| \leq \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}}\left| \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}}\right)} - \cos{(12^{n} \pi x)} \right|\)

Or, pour tout \(u\) et \(v\) de \(\mathbb{R}\), \(|\cos{(u)} - \cos{(v)}| \leq |u - v|\).

Donc :

\(\begin{array}{r c l}\left| \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left[ \cos{\left( 12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}}\right)} - \cos{(12^{n} \pi x)} \right] \right| & \leq & \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left| 12^{n} \pi x + \frac{12^{n} \pi}{2.12^{p}} - 12^{n} \pi x \right| \\ \\& \leq & \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} \left|\frac{12^{n} \pi}{2.12^{p}}\right| \\ \\& \leq & \frac{\pi}{2.12^{p}} \overset{p-1}{\underset{n=0}{\sum}} \frac{1}{2^{n}} . 12^{n} \\ \\& \leq & \frac{\pi}{2.12^{p}} \overset{p-1}{\underset{n=0}{\sum}} 6^{n} \\ \\& \leq & \frac{\pi}{2.12^{p}}~.~\frac{1-6^{p}}{1-6} = \frac{(6^{p} - 1) \pi}{5.2.12^{p}} \\ \\& \leq & \frac{6^{p} \pi}{10.12^{p}} = \frac{\pi}{10.2^{p}} \\\end{array}\)

Il vient alors : \(|\beta_{p}(x)| \geq 2.6^{p} \sqrt{2} \left| \cos{\left( 12^{p} \pi x - \frac{\pi}{4}\right)} \right| - 2.12^{p} \frac{\pi}{10 . 2^{p}} = 6^{p} \left[ 2\sqrt{2} \left| \cos{\left( 12^{p} \pi x - \frac{\pi}{4}\right) } \right| -\frac{\pi}{5} \right]\)

\(\beta_{p}(x) \geq 6^{p} \left[ 2\sqrt{2} \left| \cos{\left(12^{p} \pi x - \frac{\pi}{4}\right)} - \frac{\pi}{5} \right| \right]\)

Donc, \(\begin{array}{r c l}\textrm{max} \{ | \alpha_{p}(x), |\beta_{p}(x)| \} & \geq & \textrm{max} \left\{ 6^{p} \left[ |2\cos{(12^{p} \pi x)}| - \frac{\pi}{5}\right], 6^{p} \left[ 2\sqrt{2} \left| \cos{\left(12^{p} \pi x - \frac{\pi}{4} \right)}\right| -\frac{\pi}{5} \right] \right\} \\& \geq & 2.6^{p} \textrm{max} \left\{ |\cos{(12^{p} \pi x)}|, \sqrt{2} \left| \cos{(12^{p} \pi x - \frac{\pi}{4})} \right| \right\} - 6^{p} \frac{\pi}{5} \end{array}\)

Etudions \(y \longmapsto a(y) = |\cos{(y)}|\) et \(y \longmapsto b(y) = \sqrt{2} \left| \cos{\left( y - \frac{\pi}{4}\right)} \right|\). \(a\) et \(b\) sont périodiques de période \(\pi\).

On les étudie donc sur \(I = \left[ -\frac{\pi}{2}, \frac{\pi}{2}\right]\).

Sur \(I\), \(a(y) = \cos{(y)}\).

Sur \(\left[ -\frac{\pi}{2},-\frac{\pi}{4}\right]\), \(b(y) = -\sqrt{2} \cos{}\left( y - \frac{\pi}{4} \right) = -\cos(y) -\sin(y)\) ;

Sur \(\left[ -\frac{\pi}{4}, \frac{\pi}{2}\right]\), \(b(y) = \sqrt{2} \cos{\left( y - \frac{\pi}{4}\right)} = \cos(y) + \sin(y)\).

Donc :

• Sur \(\left[-\frac{\pi}{2},-\frac{\pi}{4}\right]\) : \(\begin{array}{r c l} a(y) - b(y) & = & 2 \cos{(y)} + \sin{(y)} \\ & = & \sqrt{5} \sin{(y + \textrm{Arctan}(2))} \end{array}\)

  Or, \(\textrm{Arctan}(2) \in \left[\frac{\pi}{4}, \frac{\pi}{2} \right]\), donc :

  \(a(y) - b(y)\) est \(\begin{array}{|l }\leq 0~~\textrm{quand}~~y \in \left[-\frac{\pi}{2}, -\textrm{Arctan}(2)\right] \\ \\ \geq 0~~\textrm{quand}~~y \in \left[-\textrm{Arctan}(2), -\frac{\pi}{4}\right] \end{array}\)

• Sur \(\left[-\frac{\pi}{4},\frac{\pi}{2}\right]\) : \(a(y) - b(y) = -\sin(y)\).

  Donc : \(a(y) - b(y)\) est \(\begin{array}{|l } \geq 0~~\textrm{quand}~~y \in \left[ -\frac{\pi}{4}, 0\right] \\ \\ \leq 0~~\textrm{quand}~~y \in \left[0, \frac{\pi}{2}\right] \end{array}\)

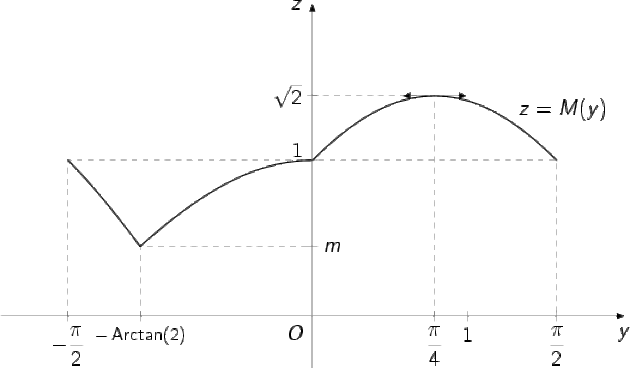
  On en déduit que : \(\textrm{max} \{a(y), b(y)\}\) =

  \(\begin{array}{|l}b(y) = -\cos{(y)} - \sin{(y)}~~\textrm{quand}~~y \in \left[-\frac{\pi}{2}, -\textrm{Arctan}(2)\right]\\ \\a(y) = \cos{y}~~\textrm{quand}~~y \in\left[-\textrm{Arctan}(2), 0\right]\\ \\b(y) = \cos(y) + \sin(y)~~\textrm{quand}~~y \in \left[0, \frac{\pi}{2}\right]\end{array}\)

  Etudions donc la fonction \(M\) définie sur \(I\) par :

  \(M(y) = \begin{array}{|l}-\cos{(y)} - \sin{(y)}~~\textrm{quand}~~y \in \left[-\frac{\pi}{2}, -\textrm{Arctan}(2)\right]\\ \\\cos{(y)}~~\textrm{quand}~~y \in \left[-\textrm{Arcan}(2), 0\right]\\ \\\cos{(y)} + \sin{(y)}~~\textrm{quand}~~y \in \left[0, \frac{\pi}{2}\right]\end{array}\)

  \(M\) est continue sur \(I\), dérivable sur \(\left[-\frac{\pi}{2}, -\textrm{Arctan}(2)\right[ \bigcup \bigg]-\textrm{Arctan}(2), 0\bigg[ \bigcup \bigg]0, \frac{\pi}{2}\bigg]\) et on a :

  \(M'(y) = \begin{array}{|l}\sin{(y)} - \cos{(y)}~~\textrm{quand}~~y \in \left[-\frac{\pi}{2}, -\textrm{Arctan}(2)\right]\\ \\-\sin{(y)}~~\textrm{quand}~~y \in \left[-\textrm{Arcan}(2), 0\right]\\ \\-\sin{(y)} + \cos{(y)}~~\textrm{quand}~~y \in \left[0, \frac{\pi}{2}\right]\end{array}\)

• Sur \(\left[-\frac{\pi}{2}, -\textrm{Arctan}(2)\right[ :\) \(\sin{(y)} < 0\) et \(\cos{(y)} \geq 0\), donc \(M'(y) < 0\).

• Sur \(\left] -\textrm{Arctan}(2), 0\right[\) : \(\sin{(y)} < 0\), donc \(M'(y) > 0\).

• Sur \(\left]0,\frac{\pi}{2}\right[\) :

  • Sur \(\left] 0, \frac{\pi}{4} \right]\) :

    \(\cos{(y)} \geq \sin{(y)}\) donc \(M'(y) \geq 0\).

  • Sur \(\left]\frac{\pi}{4}, \frac{\pi}{2}\right]\) :

    \(\cos{(y)} \leq \sin{(y)}\) donc \(M'(y) \leq 0\).

On en déduit le tableau de variations de \(M\) :

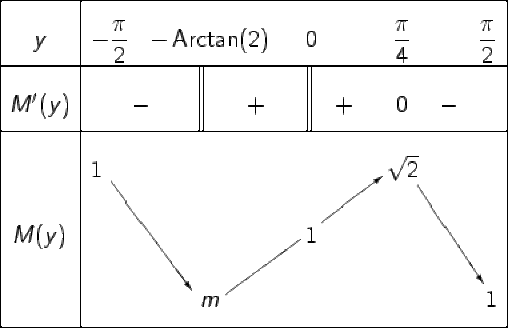
\(m = M \Big( -\textrm{Arctan}(2) \Big) = \cos{Big( -\textrm{Arctan}(2)\Big)} = \frac{1}{\sqrt{5}}\)

Ceci montre que\( \textrm{max} \{ a(y), b(y) \} \geq m = \frac{1}{\sqrt{5}}\). On en déduit, en posant \(y = 12^{p} \pi x\) : \(\textrm{max} \Bigg\{ |\cos{(12^{p} \pi x)}|, \sqrt{2} \left|\cos{(12^{p} \pi x - \frac{\pi}{4})}\right|\Bigg\} \geq \frac{1}{\sqrt{5}}\).

Or, on a vu que \(\textrm{max} \{|\alpha_{p}(x)|, |\beta_{p}(x)|\} \geq 2 . 6^{p} \textrm{max} \left\{\left|\cos{\left(12^{p} \pi x - \frac{\pi}{4}\right)}\right|\right\} - 6^{p}\frac{\pi}{5}\);

Il vient alors : \(\begin{array}{r c l} \textrm{max} \{| \alpha_{p}(x)|, |\beta_{p}(x)|\}&\geq&2.6^{p} \frac{1}{\sqrt{5}} - 6^{p}\frac{\pi}{5}\\ \\& \geq & 6^{p} \left( \frac{2}{\sqrt{5}} - \frac{\pi}{5}\right) \\ \\ & \geq & 6^{p} \frac{2\sqrt{5} - \pi}{5}\end{array}\)

Comme \(2\sqrt{5} - \pi > 0\), on en déduit que \(\underset{p \rightarrow +\infty}{\textrm{lim}} \Big(\textrm{max} \{|\alpha_{p}(x)|, |\beta_{p}(x)|\}\Big) = +\infty\).

On a donc bien montré que \(\underset{p \in \mathbb{N}}{\textrm{max}} \Big\{|\alpha_{p}(x)|, |\beta_{p}(x)|\Big\} = +\infty\); ce qui prouve, comme on l'avait remarqué au début, que \(f\) n'est pas dérivable en \(x\) ; ceci étant vrai pour tout \(x\) de \(\mathbb{R}\), \(f\) n'est donc dérivable nulle part.

Ainsi, \(f\) est continue sur \(\mathbb{R}\) et dérivable nulle part.