Travaux pratiques : diagramme de bifurcation
Le diagramme
Soit \(\begin{displaymath} \left\{ \begin{array}{ll}x'=ax+by\\y'=cx+dy\end{array} \right.\end{displaymath}\) un système de deux équations linéaires,
qu'on peut aussi écrire X' = A X, où A est la matrice \(\begin{displaymath}\left(\begin{array}{cc}a & b \\c & d\end{array}\right)\end{displaymath}\)
On a déjà étudié la nature du point stationnaire situé à l'origine suivant la valeur des valeurs propres \(\lambda_1 , \lambda_2\) de la matrice A :
Règle :
Si \(\lambda_1 , \lambda_2\) sont réelles de même signe, on a un noeud, qui est :
attractif si elles sont négatives,
répulsif si elles sont positives.
Si \(\lambda_1 , \lambda_2\) sont réelles de signe contraire, on a un col .
Si \(\lambda_1 , \lambda_2\) sont complexes conjuguées, on a
un foyer attractif si elles sont de partie réelle négative,
un centre si elles sont imaginaires pures,
un foyer répulsif si elles sont de partie réelle positive.
Ces conditions peuvent en fait s'exprimer en fonction de la somme et du produit de ces valeurs propres, qui ne sont autres que la trace et le déterminant de la matrice A,
c'est à dire \(tr(A) = a+d\) et \(det(A)=ad-bc\)
Les valeurs propres \(\lambda_1\) et \(\lambda_2\) sont les racines du polynôme caractéristique \(\lambda^2-tr(A).\lambda +det(A)\)
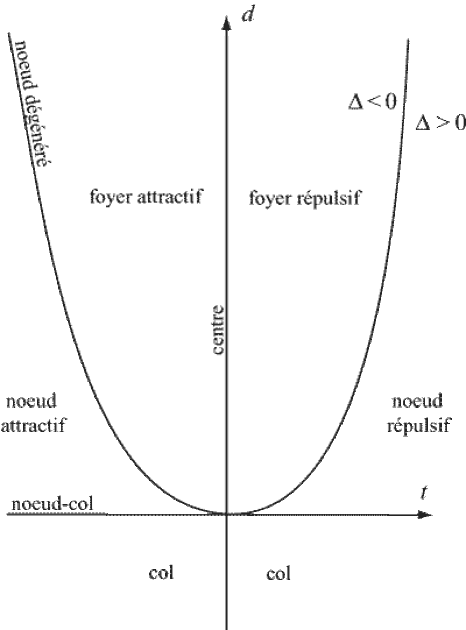
Notons \(\Delta = tr(A)^2-4.det(A)\) le discriminant de ce polynôme.
La classification suivant la nature du point stationnaire s'exprime alors comme suit :
Fondamental :
Si \(\Delta >0\) (valeurs propres réelles), alors :
si det(A) > 0, on a un nœud, qui est
attractif si tr(A) < 0,
répulsif si tr(A) > 0
si det(A) < 0, on a un col
Si \(\Delta < 0\) (valeurs propres complexes conjuguées), alors :
si tr(A) < 0, on a un foyer attractif
si tr(A) = 0 (valeurs propres imaginaires pures) on a un centre
si tr(A) > 0, on a un foyer répulsif
Allez voir les animations suivantes, qui concernent des systèmes linéaires dépendants d'un paramètre \(p\). Vous y verrez simultanément, pour chaque valeur de \(p\), l'allure du portrait de phase et la position du point\( M = (tr(A), det(A))\) dans le plan\( (t, d)\). Lorsque le point \(M\) change de région, l'allure du portrait de phase change, parfois de façon assez brusque. Ce phénomène porte le nom de bifurcation.
Animation 1
On va étudier le système suivant :
\(\begin{displaymath} \left\{ \begin{array}{ccccc}x'&=&x&+&2y\\y'&=&-2x&+&(p-1)y\end{array} \right.\end{displaymath}\)
La matrice correspondante est \(\begin{displaymath}\left(\begin{array}{cc}1 & 2 \\-2 & p-1\end{array}\right)\end{displaymath}\)
Sa trace est \(tr(A) = p\), et son déterminant est \(det(A) = p + 3\).
Explication :
Dans l'animation ci dessous, vous voyez, pour chaque valeur du paramètre \(p\) :
Sur la partie gauche : le portrait de phase correspondant, dans le plan\( (x, y)\). Les couleurs montrent le sens de parcours des trajectoires : chacune d'elles est parcourue "du bleu vers le rouge".
Sur la partie droite, qui représente le plan\( (t = tr(A), d = det(A))\), la place du point \(M\) de coordonnées\( tr(A) = p, det(A) =p+3\). Lorsque \(p\) varie, \(M\) se déplace donc sur la droite d'équation \(d = t + 3\).
Notons \(\Delta =tr (A)^2-4det (A)\)
On a tracé en rouge la parabole d'équation \(t^2 - 4 d = 0\), correspondant à \(\Delta = 0\) . Les régions dans lesquelles le portrait de phases reste du même type (noeud attractif, col, ...) sont séparées par l'axe des \(t\), le demi-axe des \(d\) positifs et la parabole.
Vous pouvez faire varier le paramètre grâce aux boutons Augmenter p et Diminuer p.
Attention :
Vous devez constater que, comme le prédit la théorie,
Si \(\Delta <0\)(à l'intérieur de la parabole : \(- 2 < p < 6\)) , on obtient :
un foyer attractif si \(tr(A) = p < 0\) \((- 2 < p < 0)\),
un centre si \(tr(A) = p = 0\).
un foyer répulsif si\( tr(A) = p > 0\) \((0 < p < 6)\),
Si \(\Delta >0\)(à l'extérieur de la parabole) , on obtient
un nœud attractif si \(tr(A) < 0\) et \(det(A) > 0\) (\(-3 < p < -2\) : \(M\) est entre l'axe des abscisses négatives et la parabole),
un nœud répulsif si\( tr(A) > 0\) et \(det(A) > 0\) (\(p > 6\) : \(M\) est à droite de la parabole),
un col si \(det(A) < 0\) (\( p < - 3\) : \(M\) est en dessous de l'axe des abscisses)
Observez ce qui se passe si \(det(A) = 0\) : on obtient alors toute une droite de points stationnaires, les autres trajectoires sont des demi-droites (démontrez-le).
Animation 2
On va étudier le système suivant :
\(\begin{displaymath} \left\{ \begin{array}{ccccc}x'&=&\frac{cos(p)}2x & +&2y\\y'&=&(\frac{cos^2(p)}4-sin(p))x & +&(p-1)y\end{array} \right.\end{displaymath}\)
La matrice correspondante est \(\begin{displaymath}\frac{1}4\left(\begin{array}{cc}2cos(p) & 4 \\2cos^2(p)-4sin(p) & 2cos(p)\end{array}\right)\end{displaymath}\)
Sa trace est \(tr(A) = cos(p)\), et son déterminant est \(det(A) = sin(p)\).
Explication :
Dans l'animation ci dessous, vous voyez, pour chaque valeur du paramètre p :
Sur la partie gauche : le portrait de phase correspondant, dans le plan \((x, y)\). Les couleurs montrent le sens de parcours des trajectoires : chacune d'elles est parcourue "du bleu vers le rouge".
Sur la partie droite , qui représente le plan\( (t = tr(A), d = det(A))\), la place du point \(M\) de coordonnées \(tr(A) = cos(p)\), \(det(A) =sin(p)\). Lorsque \(p\) varie, \(M\) se déplace sur un cercle.
Notons \(\Delta =tr (A)^2-4det (A)\)
On a tracé en rouge la parabole \(\Delta = 0\). Les régions dans lesquelles le portrait de phases reste du même type (noeud attractif, col, ...) sont séparées par l'axe des \(t\), le demi-axe des \(d\) positifs et la parabole .
Vous pouvez faire varier le paramètre grâce aux boutons Augmenter p et Diminuer p.
Attention :
Vous devez constater que, comme le prédit la théorie,
Si \(\Delta <0\) (à l'intérieur de la parabole , on obtient
un foyer répulsif si \(tr(A) = cos(p) > 0\),
un foyer attractif si \(tr(A) = cos(p) < 0\),
un centre si \(tr(A) = 0\), c.à.d. \(p=\pi /2\)
Si \(\Delta >0\) (à l'extérieur de la parabole) , on obtient
un nœud attractif si \(tr(A) < 0\) et\( det(A)\) > 0 ( \(M\) est entre l'axe des abscisses négatives et la parabole),
un nœud répulsif si \(tr(A) > 0\) et \(det(A) > 0\) (\(M\) est entre l'axe des abscisses positives et la parabole),
un col si \(det(A) = sin(p) < 0\) ( \(M\) est en dessous de l'axe des abscisses)
Observez ce qui se passe si \(det(A) = 0\) : on obtient alors toute une droite de points stationnaires, les autres trajectoires sont des demi-droites.