Théorème de Norton
Cette transformation permet de remplacer une partie d'un réseau par un générateur de courant qui lui est électriquement équivalent, de manière à simplifier les calculs ultérieurs.
Si, entre deux nœuds d'un réseau, on ajoute une nouvelle branche, celle-ci sera parcourue par le même courant que si on remplaçait le réseau par un générateur de courant :
dont le courant maximum serait égal au courant passant dans un court-circuit placé entre les deux nœuds
dont la conductance[1] interne serait la conductance du réseau "vu de ces points"
Pour calculer la conductance interne du générateur, on ne conserve que les éléments passifs[2] du réseau : chaque générateur est remplacé par sa résistance interne.
Exemple :
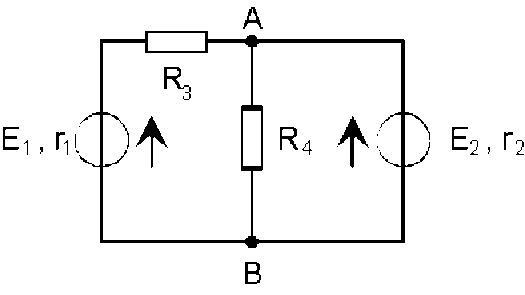
Dans le réseau ci-dessus, pour calculer l'intensité du courant traversant l'élément de résistance \(R_4\), on peut procéder en deux étapes :
calculer les caractéristiques du générateur de courant équivalent au réseau (dans lequel on a enlevé la branche contenant l'élément de résistance \(R_4\) ) "vu de \(A \textrm{ et }B\)"
remplacer le réseau par le générateur pour calculer le courant traversant l'élément de résistance \(R_4\)
Première étape :
calcul du courant de court-circuit :
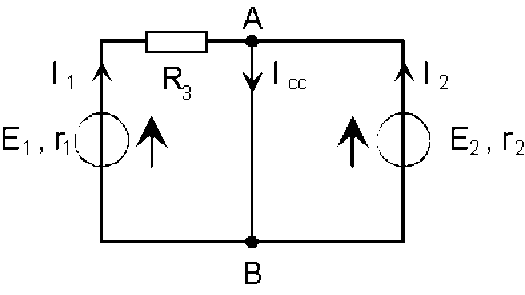
puisqu'il y a court-circuit, on peut écrire :
\(\begin{array}{lll}V_A-V_B & = & 0\\& = & E_1-(r_1+R_3).I_1\\& = & E_2-r_2.I_2\end{array}\)
d'où :
\(\displaystyle{I_1= \frac{E_1}{r_1+R_3}\textrm{ ; }I_2=\frac{E_2}{r_2}\textrm{ ; }I_{cc}=I_1+I_2=\frac{E_1}{r_1+R_3}+\frac{E_2}{r_2}}\)
soit : \(\displaystyle{I_{cc}=I_1+I_2=\frac{r_2.E_1+(r_1+R_3).E_2}{r_2(r_1+R_3)}}\)
et, en utilisant les conductances :
\(\displaystyle{I_{cc}=\frac{g_1G_3}{g_1+G_3}E_1+g_2E_2=\frac{g_1G_3E_1+g_2(g_1+G_3)E_2}{g_1+G_3}}\)
calcul de la conductance du réseau vu de \(A \textrm{ et }B\) :
on remplace les générateurs par leur résistance interne; vu des noeuds \(A \textrm{ et }B\), le réseau est formé de deux branches en parallèle, d'où sa conductance :
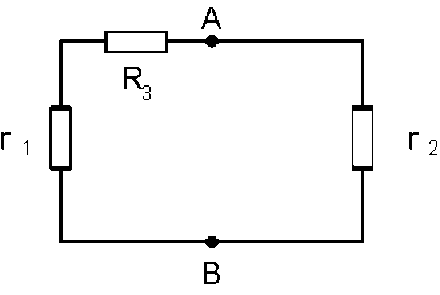
\(\displaystyle{G_{AB}=g_2+\frac{g_1G_3}{g_1+G_3}=\frac{g_1g_2+g_2G_3+G_3g_1}{g_1+G_3}}\)
Deuxième étape:
calcul du courant traversant l'élément de résistance \(R_4\) :
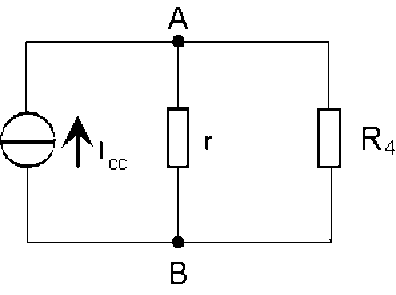
on remplace le réseau par un générateur de courant, débitant un courant maximum \(I_{cc}\), et de conductance interne \(g = G_{AB}\); l'ensemble \((r, R_4)\) constitue un diviseur de courant[3] ; d'où l'intensité du courant :
\(\displaystyle{I_4=I_{cc}\frac{G_4}{G_{AB}+G_4}}\) \(=\displaystyle{I_{cc}\frac{G_4(g_1+G_3)}{g_1g_2+g_1G_3+g_2G_3+g_1G_4+G_3G_4}}\)
En remplaçant \(I_{cc}\) par son expression en fonction de \(E_1\) et \(E_2\) :
\(\displaystyle{{I}_{{4}}=\frac{{{g}_{{1}}{G}_{{3}}{E}_{{1}}+{g}_{{2}}{\left({g}_{{1}}+{G}_{{3}}\right)}{E}_{{2}}}}{{{g}_{{1}}+{G}_{{3}}}}}\).\(\displaystyle{\frac{{{G}_{{4}}{\left({g}_{{1}}+{G}_{{3}}\right)}}}{{{g}_{{1}}{g}_{{2}}+{g}_{{1}}{G}_{{3}}+{g}_{{2}}{G}_{{3}}+{g}_{{1}}{G}_{{4}}+{G}_{{3}}{G}_{{4}}}}}\)
\(=\displaystyle{{G}_{{4}}\frac{{{g}_{{1}}{G}_{{3}}{E}_{{1}}+{g}_{{2}}{\left({g}_{{1}}+{G}_{{3}}\right)}{E}_{{2}}}}{{{g}_{{1}}{g}_{{2}}+{g}_{{1}}{G}_{{3}}+{g}_{{2}}{G}_{{3}}+{g}_{{1}}{G}_{{4}}+{G}_{{3}}{G}_{{4}}}}}\)
Et, en remplaçant les conductances par leurs expressions en fonction des résistances, on obtient, comme pour les autres méthodes :
\(I_{4} = \frac{r_{2}E_{1} + (r_{1}+R_{3})E_{2}}{r_{1}r_{2} + r_{1}R_{4} + r_{2}R_{3} + r_{1}R_{4} + R_{3}R_{4}}\)