Méthodes de Maxwell Méthode des potentiels de noeud
Méthode :
Dans le réseau, on choisit un des nœuds comme origine des potentiels, et on prend comme inconnues les potentiels des autres nœuds. On exprime ensuite les intensités[1] des courants dans chacune des branches en fonction de la différence de potentiel[2] aux bornes, puis on écrit les équations aux nœuds.
Exemple :
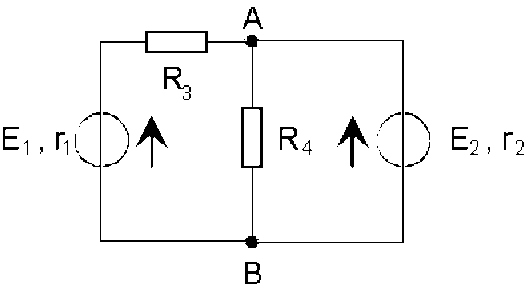
Dans le réseau ci-dessus, pour calculer l'intensité du courant traversant l'élément de résistance[3] \(R_4\), on peut procéder comme suit :
on choisit B comme origine des potentiels ; la seule inconnue est alors \(V_A\).
on choisit un sens (arbitraire) pour le courant dans chacune des branches, par exemple de \(B\) vers \(A\).
on calcule les intensités des courants dans chacune des branches en fonction de la différence de potentiel aux bornes :
branche de gauche : \(\displaystyle{{V}_{{A}}={E}_{{1}}-{\left({r}_{{1}}+{R}_{{3}}\right)}.{I}_{{1}}\textrm{ ; }{I}_{{1}}=\frac{{{E}_{{1}}-{V}_{{A}}}}{{{\left({r}_{{1}}+{R}_{{3}}\right)}}}}\)
branche centrale : \(\displaystyle{{V}_{{A}}=-{R}_{{4}}.{I}_{{4}} \textrm{ ; } {I}_{{4}}=-\frac{{V}_{{A}}}{{R}_{{4}}}}\)
branche de droite : \(\displaystyle{{V}_{{A}}={E}_{{2}}-{r}_{{2}}.{I}_{{2}} \textrm{ ; } {I}_{{2}}=\frac{{{E}_{{2}}-{V}_{{A}}}}{{r}_{{2}}}}\)
[on peut aussi utiliser les conductances[4], ce qui donne : \(\displaystyle{{I}_{{1}}=\frac{{{g}_{{1}}{G}_{{3}}}}{{{g}_{{1}}+{G}_{{3}}}}{\left({E}_{{1}}-{V}_{{A}}\right)}}\) ; \(\displaystyle{{I}_{{4}}=-{G}_{{4}}.{V}_{{A}}}\) ; \({I}_{{2}}={g}_{{2}}.{({E}_{{2}}-{V}_{{A}})}\)
on écrit les équations aux noeuds; il n'y en a qu'une :
\(I_1+I_2+I_4=0\)
\(\displaystyle{\frac{{{E}_{{1}}-{V}_{{A}}}}{{{r}_{{1}}+{R}_{{3}}}}+\frac{{{E}_{{2}}-{V}_{{A}}}}{{r}_{{2}}}-\frac{{V}_{{A}}}{{R}_{{4}}}={0}}\)
que l'on peut résoudre en prenant comme inconnue soit \(V_A\), soit \(I_4\) ; finalement :
\(\displaystyle{{I}_{{4}}=\frac{{{E}_{{1}}.{r}_{{2}}+{E}_{{2}}.{\left({r}_{{1}}+{R}_{{3}}\right)}}}{{{r}_{{1}}{r}_{{2}}+{r}_{{1}}{R}_{{4}}+{r}_{{2}}{R}_{{3}}+{r}_{{2}}{R}_{{4}}+{r}_{{3}}{R}_{{4}}}}}\)
ou, en fonction des conductances :
\(\displaystyle{{I}_{{4}}={G}_{{4}}\frac{{{g}_{{1}}{G}_{{3}}.{E}_{{1}}+{g}_{{2}}{\left({g}_{{1}}+{G}_{{3}}\right)}.{E}_{{2}}}}{{{g}_{{1}}{g}_{{2}}+{g}_{{1}}{G}_{{3}}+{g}_{{1}}{G}_{{4}}+{g}_{{2}}{G}_{{3}}+{G}_{{3}}{G}_{{4}}}}}\)