Description mathématique / Types de densité
Densité volumique de charges
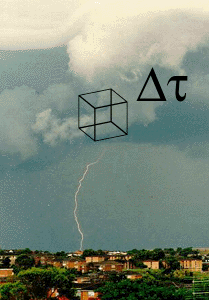
Lorsque le corps électrisé est un volume \(W\) contenant des charges indiscernables à l'échelle macroscopique, il est commode de définir une densité volumique de charges, notée \(\rho\) ,définie de la façon suivante : on découpe le volume \(W\) en éléments \(\Delta \tau\) très petits. Si on considère l'un de ces éléments \(\Delta \tau\) situé autour d'un point \(M\), il contient la charge \(\mathrm d Q\).
On dira que la densité volumique de charges existant localement autour du point \(M\) est :
\(\displaystyle{\rho=\lim_{\Delta \tau \rightarrow 0} \frac {\Delta Q} {\Delta\tau} = \frac{\mathrm dQ}{\mathrm d\tau} ~ \mathrm{C.m}^{-3}}\) (Coulomb par mètre cube)
Densité superficielle de charges
Dans de nombreux cas, les charges sont réparties sur une épaisseur très faible par rapport aux autres dimensions et peuvent donc être considérées comme réparties en surface. Ceci nous permet de définir et de définir une densité superficielle de charges \(\sigma\) telle que :
\(\displaystyle{\sigma = \lim_{\Delta S \rightarrow 0} \frac{\Delta Q}{\Delta S} = \frac{\mathrm dQ}{\mathrm dS} ~ \mathrm{C.m}^{-2}}\) ( Coulomb par mètre carré )
Densité linéique
Il peut arriver qu'une dimension du corps chargé soit très supérieure aux deux autres, c'est à dire que la charge semble répartie sur un fil.
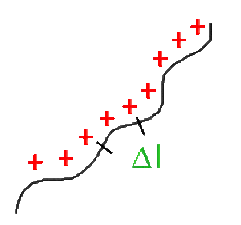
Il est alors commode de définir une densité linéique de charges notée \(\lambda\) telle que :
\(\displaystyle{\lambda = \lim_{\Delta l \rightarrow 0} \frac{\Delta Q}{\Delta l} = \frac{\mathrm dQ}{\mathrm dl} ~ \mathrm{C.m}^{-1}}\) ( Coulomb par mètre )