Densité volumique / Densité variable 2/4
Partie
Question
Un nuage de charges cylindrique de hauteur \(H\) et de rayon \(R\) est chargé par une densité volumique de charges \(\rho = \frac{k}{r}\) variable en fonction du rayon \(r\) dans le cylindre, \(0 < r \le R\).
Donner l'expression littérale de la charge \(Q\) contenue dans le volume \(\Omega\) de ce cylindre.
Aide simple
Sur quel volume élémentaire \(\mathrm d \tau\) du cylindre la densité volumique de charges peut-elle être considérée approximativement constante ? (Remarquez que \(\rho\) ne dépend que de \(r\) et pas de l'orientation autour de l'axe du cylindre)
Aide détaillée
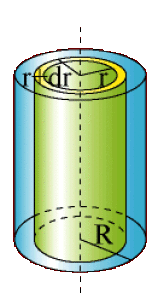
Le volume élémentaire \(\mathrm d \tau\) compris entre les cylindres \((r,H)\) et \((r + \mathrm d r , H)\) est tel que la densité volumique de charges qu'il contient peut être considérée constante puisque \(dr\) est infiniment petit
Aussi, l'intégrale : \(Q = \iiint_{\Omega} \rho \mathrm d \tau\)
sur un volume se réduit à une intégrale simple en \(\mathrm d r\)
Solution simple
\(Q= 2 k \pi R H\)
Solution détaillée
La densité \(\rho\) ne dépend que du rayon \(r\) dans le cylindre. Donc, à la même distance \(r\) de l'axe du cylindre et sur toute la hauteur \(H\), la densité volumique de charges est constante
Aussi nous choisirons comme volume élémentaire \(\mathrm d \tau\) sur lequel \(\rho\) peut être considéré constant, le cylindre élémentaire compris entre le cylindre \((r,H)\) et le cylindre \((r + \mathrm d r , H)\).
Le volume du cylindre \((r,H)\) est alors : \(\tau = \pi r^2 H\) et \(\mathrm d \tau\) est obtenue en faisant la différentielle de cette expression : \(\mathrm d \tau = 2 \pi r H\)
(C'est aussi le périmètre de la couronne cylindrique multiplié par son épaisseur et sa hauteur)
La charge \(Q\) totale contenue dans le volume \(\Omega\) du cylindre s'écrit :
\(\displaystyle{Q = \iiint _{\Omega} \rho \mathrm d \tau = \int_0^R \rho 2 \pi r H ~ \mathrm d r}\)
\(\Omega =\) Volume total du cylindre
\(\displaystyle{Q = \int_0^R \frac{k 2 \pi r H \mathrm d r}{r}}\) ; \(Q=2 k \pi r H\)