Définition
Soit une charge \(Q_+\) fixe. Pour maintenir une charge mobile \(q_+\) à la distance \(r\) de la source, il faut exercer sur elle une force extérieure \(\vec F_{ext} = - q \vec E\) opposée à la force électrostatique.
Le travail de \(\vec F_{ext}\) sur un contour (\(AB\)) ne dépend pas du trajet suivi, il ne dépend que des distances \(r_A\) et \(r_B\).
DEMONSTRATION
\(W_{AB} = - \int_B^A q \vec E. \mathrm d \vec M = \frac{Qq} {4 \pi \varepsilon_0 r_A} - \frac {Qq} {4 \pi \varepsilon_0 r_B}\)
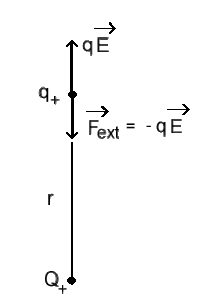
Le travail \(W_{AB}\) ne dépendant pas du trajet suivi, \(W_{AB}\) est emmagasiné sous forme d'énergie potentielle
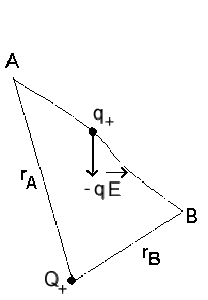
\(\displaystyle{W_{AB} = - \int_B^A q \vec E. \mathrm d \vec M} = {E_p} _{A} - {E_p} _{B}\)
avec
\(E_p = \frac {Q~q} {4 \pi \varepsilon_0 r}\)
On pose
\(E_p = q . V\) ,
V étant appelé potentiel électrostatique.
D'où : \(~~\displaystyle{W_{AB} = - \int_B^A q \vec E. \mathrm d \vec M} = q\big(V_{A} - V_{B}\big)\)
La définition de la différence de potentiel entre deux points est donc la suivante :
\(\displaystyle{V(A) - V(B) = - \int_B^A \vec E. \mathrm d \vec M}\)
Unité : le potentiel électrostatique s'exprime en volts.