Effet dipolaire

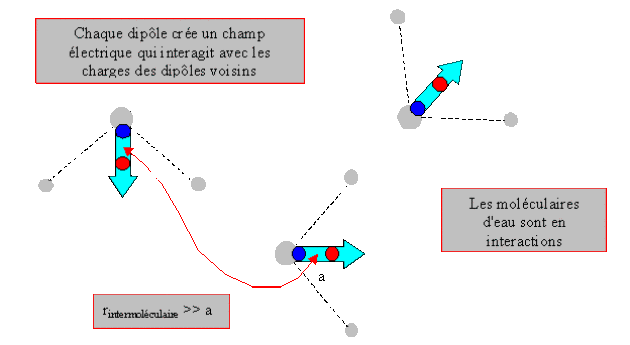
Objectif de ce travail : Déterminer les interactions entre deux molécules présentant un moment dipolaire permanent ou induit.

Calculons le potentiel créé par le dipôle en un point \(M\) de l'espace afin de connaître le champ créé par un dipôle au niveau d'un dipôle voisin.

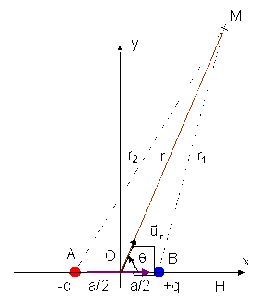
Un point \(M\) d'un repère orthonormé \(xOy\) d'origine \(O\) milieu de \(AB = a. OM\) est caractérisé dans le plan par sa distance \(r_1\) à la charge \(+q\), et sa distance \(r_2\) à la charge \(- q\). \(M\) est défini par ses coordonnées cartésiennes \(M(x_M, y_M)\). \(M\) peut aussi être défini par ses coordonnées cylindriques \(M(r, \theta)\).

Comme dans le cas d'une distribution de charges, le potentiel électrique créé en \(M\) de l'espace par l'ensemble des deux charges du dipôle est égal à la somme algébrique des potentiels créés par la charge \(+q\) et par la charge \(-q\) en ce point \(M\).

Dans un repère \(xOy\) dont l'origine \(O\) est le milieu de \(AB = a\), on désigne par \(r_1\) la distance de la charge \(+q\) à \(M\) et par \(r_2\) la distance de la charge \(-q\) à \(M\).

Si le point \(M\) peut être défini par ses coordonnées cartésiennes \(x_M\) et \(y_M\) dans le repère \(xOy\), il possède également des coordonnées polaires \(r\) et \(\theta\) comme représentées sur la figure ci-dessous.

Outre ces précisions géométriques, il est important de mentionner que dans la réalité la distance \(a\) est très inférieure à la distance \(OM = r\). Les quelques exemples de dipôles déjà étudiés ont montré que \(a\) est de l'ordre de \(1/100\) d'Angström, tandis que nous nous intéressons au potentiel que crée un dipôle au niveau d'un autre dipôle dont la distance \(r\) est de l'ordre des distances intermoléculaires soit l'Angström. Nous aurons donc toujours :

\(a \ll r\).

En explicitant l'identité remarquable : \(r_2^2 - r_1^2 = \big(r_2 + r_1\big) ~ \big(r_2 - r_1\big)\)

il vient : \(r_2^2 - r_1^2 = x^2 + ax + \frac{a^2}{4} + y^2 ~ - x^2 + ax - \frac{a^2}{4} - y^2\)

soit : \(r_2^2 - r_1^2 = 2 a x\)

En remarquant par ailleurs que \(OH = x_M = r~.~\cos \theta\) , nous avons :

\(r_2^2 - r_1^2 = \big(r_2 + r_1\big) ~ \big(r_2 - r_1\big) = 2a.r.\cos \theta\)

Cette relation permet d'écrire que : \(r_2 - r_1 = \frac{2ar~\times~\cos \theta}{r_1 ~ + ~ r_2}\).

Nous avons déjà évoqué le fait que nous avons toujours expérimentalement \(a \ll r\). Cette situation a également pour conséquence que \(r_1\) et \(r_2\) sont proches de la valeur de \(r\).

Ainsi nous avons : \(r_1 + r_2~\#~2r\) et \(r_1.r_2~\#~r^2\) .

A l'aide de ces approximations qui seront encore une fois toujours justifiées expérimentalement, nous pouvons écrire :

\(r_2 - r_1 ~ \# ~ \frac{2ar~\times~\cos \theta}{2r}\)

et \(V(M)=\frac{q}{4 \pi \epsilon_0}\left[\frac{r_2 - r_1}{r_1 \times r_2}\right]~\#~\frac{q}{4 \pi \epsilon_0}\frac{2ar.\cos \theta}{2r^3}\)

soit : \(V(M)~\#~\frac{q}{4 \pi \epsilon_0} \frac{a.\cos \theta}{r^2}\)

Comme nous avons pu le faire à propos des forces de Coulomb et du champ Coulombien, définissons le vecteur unitaire d'origine \(O\) :

\(\vec u_r = \frac{\overrightarrow{OM}}{ \Big| \overrightarrow{OM} \Big| }\) 

Si nous rapprochons l'expression vectorielle du dipôle :

\(\vec p = q ~ \vec a~\) du terme \(~q a . \cos \theta\) ,

il apparaît que celui-ci représente la projection du vecteur moment dipolaire selon la direction \(OM\) qui porte le vecteur unitaire \(\vec u_r\). Nous avons ainsi :

\(\vec p . \vec u_r = q a . \cos \theta\)

Ce produit scalaire nous permet de simplifier et de condenser l'expression de \(V(M)\), le potentiel électrique créé par le dipôle en \(M\), sous la forme :

\(V(M) ~ = ~ \frac{1}{4 \pi \epsilon_0} \frac{\vec p . \vec u_r}{r^2}\)